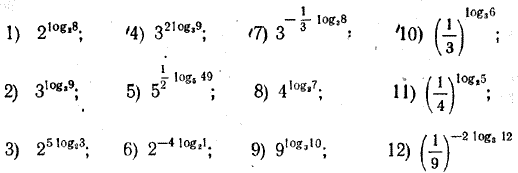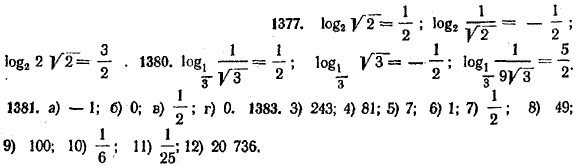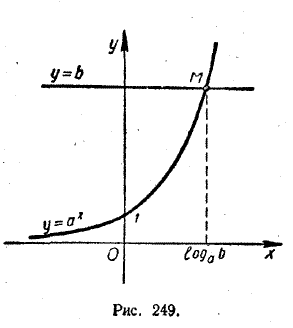
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ   VIII

§ 180 Логарифм числа по данному основанию

Алгебру иногда называют «арифметикой семи действий», желая этим подчеркнуть, что, кроме четырех арифметических действий (сложения, вычитания, умножения и деления), она рассматривает также возведение в степень и два обратных к нему действия.

Обозначим основание степени через а, показатель через х, степень через  b.  Тогда можно написать:

b = а^x.                   (1)

«Пятое» алгебраическое действие — возведение в степень — состоит в нахождении числа b по известным а и х. Это действие мы подробно изучили в главе IV (часть I), о нем говорилось также в начале этой  главы.

«Шестое» алгебраическое действие состоит в нахождении числа а по известным значениям b и х. Возводя обе части равенства (1)   в  степень ¹/_x (если только х =/= 0), получаем:

а = b^1/x.

Поэтому «шестое» алгебраическое действие легко сводится к «пятому».

Теперь мы переходим к изучению «седьмого» алгебраического действия — нахождению показателя х по известным значениям степени b и основания а. Эта задача по существу состоит в том, чтобы решить уравнение

а^x = b,                   (2)

где а и b — некоторые заданные, а x — неизвестная величина. Сразу же заметим, что данная задача разрешима    не   всегда.

Если, например, в уравнении (2) число а положительно, а число b отрицательно, то это уравнение корней не имеет. Но если только а и b положительны и а =/=1, то оно непременно имеет и притом только один корень. Напомним, что график показательной функции у = а^x обязательно пересекается с прямой у = b и притом лишь в одной точке (см. рис. 249). Абсцисса точки пересечения и  предетавляет собой корень уравнения (2).

Корень уравнения (2) принято обозначать log_ab (читается: логарифм числа b по основанию а).

Логарифм числа b по основанию а есть показатель степени, в которую нужно возвысить число а, чтобы получить число b:

а ^logab  = b.

Примеры.

1)  2⁴ = 16,  поэтому  log₂16 = 4.

2)  2 ^—3 = ¹/₈,  поэтому log₂ ¹/₈ = —3.

3)  6⁰ = 1,   поэтому   log₆ 1 = 0.

С логарифмами мы сталкиваемся при решении целого ряда прикладных задач. В качестве примера рассмотрим следующую задачу.

Как мы знаем, распад радия приближенно описывается формулой   (см.   §   178):

т (t) = т(0) • (0,9996)^t,

где т(0) — первоначальное количество радия в граммах, a m(t) —  количество радия (также в граммах) через t лет. Выясним, каков период полураспада радия, то есть через сколько лет количество  радия   уменьшается   вдвое.

Искомое число лет t является корнем уравнения

т(0) • (0,9996)^t = 0,5т (0),

или

(0,9996)^t = 0,5.

Поэтому

t = log_0,9996 0,5.

В дальнейшем мы научимся находить такие логарифмы с помощью специальных таблиц, а пока нам придется принять на веру,   что

log_0,9996 0,5 ≈ 1600.

Таким образом, количество радия уменьшается вдвое примерно через каждые  1600 лет.

Упражнения

1375. Данные равенства записать в виде логарифмических равенств (например,3² = 9  —> log₃9 = 2):

а)  2² = 4;           в) 4⁴ = 256;           д) 2^—2 = ¹/₄;

б)  3³ = 27;         г) 5³ = 125;            е) 3^—4 = ¹/₈₁;

ж)  7⁰ = 1;         и) 8^2/3   = 4;          л) 8⁰= 1;

з)   4^1/2 = 2;        к) ³√27 = 3;          м) ³√8= 2.

1376.  Проверить справедливость следующих равенств:

а)  log₄16 = 2;         в) log₅125 = 3;         д) log₃ ¹/₈₁ = — 4;

б)   log₃ 243 = 5;       г) log₇¹/₄₉ = — 2;      е) log₁₀1 = 0.

1377.   Найти  логарифмы  следующих   чисел   по  основанию  2:

4;  16; 32;  1; 0,5; 0,125; √2 ;    ¹/_√2 ;  2√2

1378.   Найти логарифмы следующих  чисел  по основанию ¹/₂

1; 2; 8; 32; 0,25; ¹/₁₆;   ¹/_√2 ;  √2;   4√2

1379.  Найти  логарифмы  следующих   чисел   по  основанию  3:

3; 1; 27; 81; ¹/₉ ; ¹/₂₄₃; √3 ; ¹/_√3  ; 3√3

1380.   Найти  логарифмы следующих  чисел   по основанию ¹/₃

¹/₃;   ¹/₂₇;   ¹/₈₁;  3;  27;   ¹/_√3;  √3 ;  ¹/_9√3

1381.  Вычислить:

а) log₂ (sin ^π/₆);        в) log₃ (tg ^π/₃);

б) log₂ (sin ^π/₂);         г) log₃ (tg ^π/₄),

1382.  Доказать тождество

log_an (a)^m = ^m/_n

Используя это тождество, вычислить:

а)  log₈ 16;               г) log₁₆64;        ж) log_1/5 125;

б)  log₂2√2;         д)  log₃27;         з) log₄ (sin ^π/₄);

в) log_√2 ¹/₂;           e) log₂₇ 243;     и) log₉  (tg ^π/₆ ).

1383.  Используя основное логарифмическое тождество а ^logab  = b  вычислить:  

1384. Доказать,   что  при  любом  положительном  a =/= 1

log_a (sin 1°) • log_a (sin 2°) ... log_a (sin 89°) • log_a (sin 90°) = 0.

ОТВЕТЫ