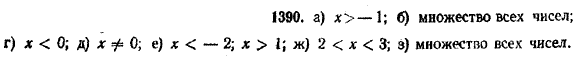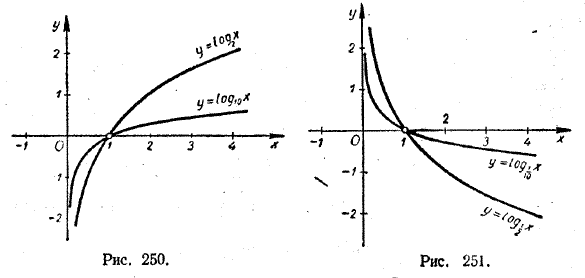
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ   VIII

§ 182 Основные   свойства   логарифмической   функции

В этом параграфе мы изучим основные свойства логарифмической   функции

y =  log_ax          (1)

Напомним, что под а в формуле (1) мы подразумеваем любое фиксированное положительное число, отличное от 1.

Свойство 1. Областью определения логарифмической функции служит множество всех положительных чисел.

Действительно, пусть b есть произвольное положительное число. Покажем, что выражение  log_ab определено. Как мы знаем, log_ab  есть не что иное, как корень уравнения

а^z = b                (2)

Если а и b — положительные числа, причем а =/= 1, то такое уравнение по свойствам 2 и 5 показательной функции (см. § 179) всегда имеет и притом только один корень. Этим корнем и является log_ab. Следовательно, log_ab в данном случае определен.

Покажем теперь, что если b < 0, то выражение log_ab не определено.

Действительно,  если бы это выражение имело смысл, то оно давало бы корень  уравнения (2); в таком случае должно было бы  выполняться   равенство

а ^logab  = b.

На самом же деле это равенство не выполняется, поскольку левая его часть представляет собой положительное, а правая — отрицательное  число  или   нуль.

Итак, выражение log_ab (а > 0, а =/=1) определено для всех положительных значений b, но не определено ни для какого отрицательного значения b, ни для b = 0. А это и означает, что областью определения функции y =  log_ax  является множество всех  положительных чисел.

1-е свойство логарифмической функции доказано. Геометрическая интерпретация этого свойства заключается и том, что график функции y =  log_ax  целиком расположен в правой полуплоскости, которая соответствует только положительным значениям х (см. рис. 250 и 251).

Свойство 2. Областью изменения логарифмической функции служит множество всех чисел.

Это означает, что выражение log_ax при различных значениях х может принимать любые числовые значения.

Пусть b — произвольное действительное число. Покажем, что существует число х,  которое удовлетворяет условию

log_ax = b.                  (3)

Тем самым и будет доказано свойство 2.

Соотношение (3) означает то же самое, что и соотношение

а^b = x.

Число а — положительное. А степень любого положительного числа с произвольным показателем всегда определена. Поэтому, выбрав в качестве искомого значения х число а^b , мы и удовлетворим   условию (3).

Свойство 3. При а > 1 логарифмическая функция y =  log_ax  является монотонно возрастающей, а при 0 < а < 1 — монотонно убывающей.

Пусть а > 1 и х₂ > х₁. Докажем, что  

log_ax₂  > log_ax₁ .

Для доказательства предположим противное:  log_ax₂ < log_ax₁  или  log_ax₂  = log_ax₁. При а > 1 показательная функция у = а^x  монотонно возрастает.   Поэтому из условия log_ax₂< log_ax₁  вытекает, что а ^{loga x2}  < а ^{loga x1}, Но а ^{loga x2} = x₂ ,  а ^{loga x1} = x₁. Следовательно, x₂ < x₁. А это противоречит условию, согласно которому x₂ > x₁, К противоречию приводит и другое предположение:  log_ax₂  = log_ax₁.   В   этом   случае   должно   было   бы   быть а ^{loga x2}  < а ^{loga x1}  или  x₂ = x₁.   Остается   признать,   что

log_ax₂  > log_ax₁.

Тем самым мы доказали, что при а > 1 функция у = log_ax является  монотонно возрастающей.

Случай, когда а < 1, предлагаем учащимся рассмотреть самостоятельно.

3-e свойство логарифмической функции допускает простую геометрическую интерпретацию. При а > 1 график функции у = log_ax  с ростом х все выше и выше поднимается (см. рис. 250), а при а < 1 он с ростом х все ниже и ниже опускается (см. рис.   251).

Следствие. Если логарифмы двух чисел по одному и тому же положительному основанию, отличному от 1, равны, то равны и сами эти числа.

Другими  словами,   из  условия

log_ax = log_ay (a > 0, а =/= 1)

вытекает, что

х = у.

Действительно, если бы одно из чисел х и у было больше другого, то в силу монотонности логарифмической функции одно из чисел log_ax и log_ay было бы больше другого. Но это не так. Следовательно,  х = у.

Свойство 4. При х =1 логарифмическая функция у = log_ax принимает значение, равное нулю.

Графически это означает, что независимо от а кривая у = log_ax  пересекается с осью х в точке с абсциссой х = 1 (см. рис.   250  и  251).

Для доказательства 4-го свойства достаточно заметить, что при   любом   положительном а

а⁰ = 1.

Поэтому   log_a 1 = 0.

Свойство 5. Пусть а > 1. Тогда при х > 1 функция у = log_ax принимает положительные, а при 0 < х < 1 — отрицательные значения.

Если же 0 < а <  1, то, наоборот, при х > 1 функция у = log_ax принимает отрицательные, а при 0 < х  < 1 — положительные значения.

Это свойство логарифмической функции также допускает простую графическую интерпретацию. Пусть, например, а >1. Тогда та часть кривой у = log_ax, которая соответствует значениям х > 1, располагается выше оси х, а та часть этой кривой, которая соответствует значениям 0 < х  < 1, находится ниже оси х (см. рис. 250). Аналогично может быть интерпретирован и случай,   когда   a < 1   (рис.   251).

5-е свойство логарифмической функции является простым следствием 3-го и 4-го свойств. Для определенности рассмотрим случай, когда а > 1. Тогда по 3-му свойству функция у = log_ax будет монотонно возрастающей. Поэтому если х > 1,то log_ax >  log_a 1. Но по 4-му свойству log_a 1= 0. Следовательно, при х >1  log_ax > 0. При х < 1 log_ax <  log_a1,  то   есть  log_ax < 0.

Аналогично может быть рассмотрен и случай, когда а < 1. Учащимся предлагается разобрать его самостоятельно.

К рассмотренным пяти свойствам логарифмической функции мы без доказательства добавим еще одно свойство, справедливость которого наглядно отражается на рисунках 250 и 251.

Свойство 6. Если а >1, то при х —> 0 значения функции у = log_ax неограниченно убывают (у —> — ∞). Если 0 < а < 1, то при х —> 0 значения функции у = log_ax неограниченно возрастают (у —>  ∞).

Упражнения

1390. Найти области определения следующих функций:

а)  y = log₂( 1 + х);                д) y = log₇ |x|;

б) y = log_1/3 (х² + 1);            е) y = log₃ (x²+ x —  2);

в)  y = log₁₀ (4 + х² )           ж) y = log_0,5 (5x — x² — 6);

 г) y = log₅ (—х);                 з)   y = log₆ (x² + x+ 1).

1391.  Для каких значений х в интервале  0 < х < 2π определены выражения:

а)  log₂(sin х);                    в) log₄(tg х);

б)  log₃(cos х);                   г) log₅(ctg х)?

1392.   Что  вы  можете сказать  о  наибольших  и  наименьших значениях функций:

а)   y = log₂ x;                     б)   y = | log₂ x |?

1393.   На основании  какого свойства логарифмической функции можно утверждать, что

a) log₁₀ 5 > log₁₀ 4;         б) log_0,1 5 < log_0,1 4?

1394.   Какое число больше:

а)   log₂5 или  log₂6;            в) log_1/3 2 или   log_1/3 4;

б)  log₅ ¹/₂ или  log₅ ¹/₃;           г) log_1/7 ⁴/₅  или  log_1/7 ⁵/₆?

1395.  Решить  относительно  х   неравенства:

а)  log₂ х > log₂ 3;            г)  log_1/2  (3х) <  log_1/2 6;

б)  log₃ х² >  log₃ 4;          д) log₁₀  (х² — 1) > log₁₀ (4х + 4);

в) log_1/3 х > log_1/3 2;             e) log_0,1 (1 — х²) > log_0,1(2х + 2).

1396. Что можно сказать о числе а, если

а)  log_a7 >  log_a6;              в)  log_a ¹/₃ <  log_a ¹/₂;

б)   log_a5 <  log_a4;            г)  log_a5 > 0?

1397.  Что можно сказать о числе а, если при   любых  значениях х

 log_a (х²+ l) >  log_a х?

1398.  Между какими последовательными  целыми   числами  заключены логарифмы:

a) log₂ 5;         б) log₃ 8;         в)  log_1/3 7;         г)  log_1/2 9?

1399.   Какие из данных  чисел  являются  положительными  и какие  отрицательными:

а)   log₂ 5;         в) log_1/2 5;      д)  log₇ 1;         ж) log_π/34;

б)   log₂ ¹/₃;      г) log_1/3 ¹/₂;    е) log_π 3;         з) log_π/4 4?

ОТВЕТЫ