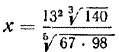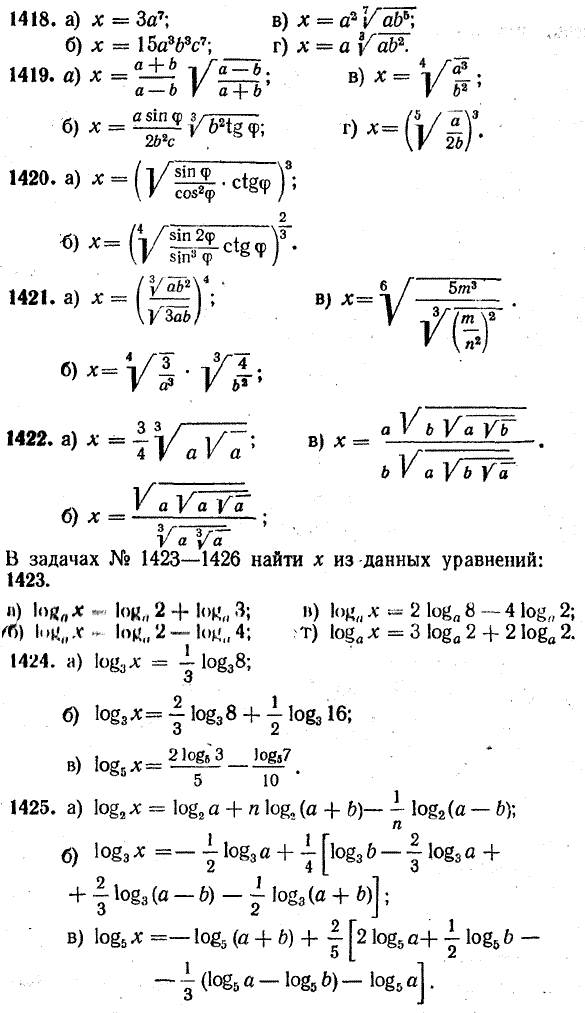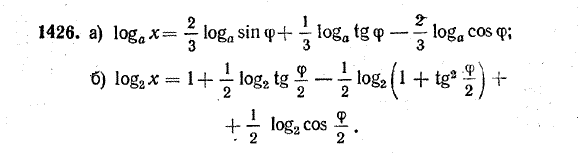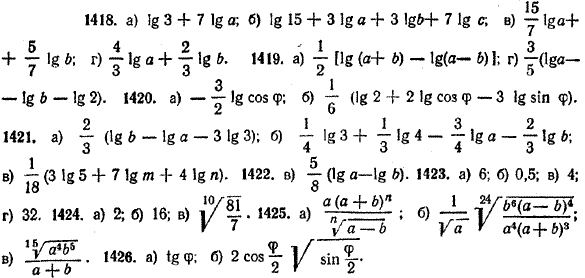ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ   VIII

§ 186. Логарифмирование и  потенцирование

Если некоторое выражение составлено из положительных чисел посредством умножения, деления, возведения в степень и извлечения корня, то логарифм всего этого выражения легко выразить через логарифмы входящих в него чисел.

Пусть,   например,

Тогда по теореме о логарифме дроби

log_ax = log_a(13^{2  3}√140) —  log_a⁵√67 • 98

Теорема о логарифме произведения дает:

log_a(13^{2  3}√140)  = log_a13²  + log_a ³√140,

 log_a⁵√67 • 98 =  log_a⁵√67 +  log_a⁵√98

Теперь, используя теоремы о логарифме степени и корня, получаем:

log_a13² = 2  log_a13,                log_a⁵√67  = ¹/₅ log_a67,

log_a ³√140 = ¹/₃ log_a 140,         log_a⁵√98  = ¹/₅ log_a 98.

Таким образом,

log_ax  = 2  log_a13 + ¹/₃ log_a 140 — ¹/₅ log_a67 — ¹/₅ log_a 98.

Переход от выражения к его логарифму называется логарифмированием этого  выражения.

Операция, обратная логарифмированию, называется потенцированием. Она заключается в том, что по логарифму некоторого выражения восстанавливается само выражение. Поясним это на следующем примере. Пусть

log_ax = 2 log_a10 — ¹/₂ log_a7 — 3 log_a 3 + ¹/₃ log_a19.

Прежде всего, используя теоремы о логарифме степени и корня, можно записать:

2 log_a10 =  log_a10² = log_a100,

¹/₂ log_a7 = log_a(7)^1/2 = log_a√7,

3 log_a 3 = log_a 3³= log_a 27,

¹/₃ log_a19 = log_a(19)^1/3  = log_a ³√19

После этого log_ax можно записать в виде

log_ax = log_a100 —   log_a√7 — log_a 27 + log_a ³√19

Теперь, используя теоремы о логарифме произведения и частного, получим:

log_ax = (log_a100 + log_a ³√19 ) — (log_a√7  + log_a 27 ) =

= log_a(100 • ³√19) — log_a (√7 •  27) = log_a  .

Итак,

log_ax = log_a

Но если логарифмы двух положительных чисел по одному и тому же основанию равны, то равны и сами эти числа.  Поэтому

x =  

Упражнения

Прологарифмировать по основанию 10 следующие выражения (№ 1418 — 1422):

ОТВЕТЫ