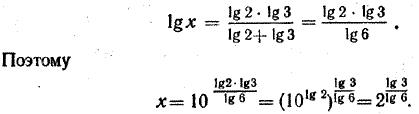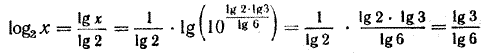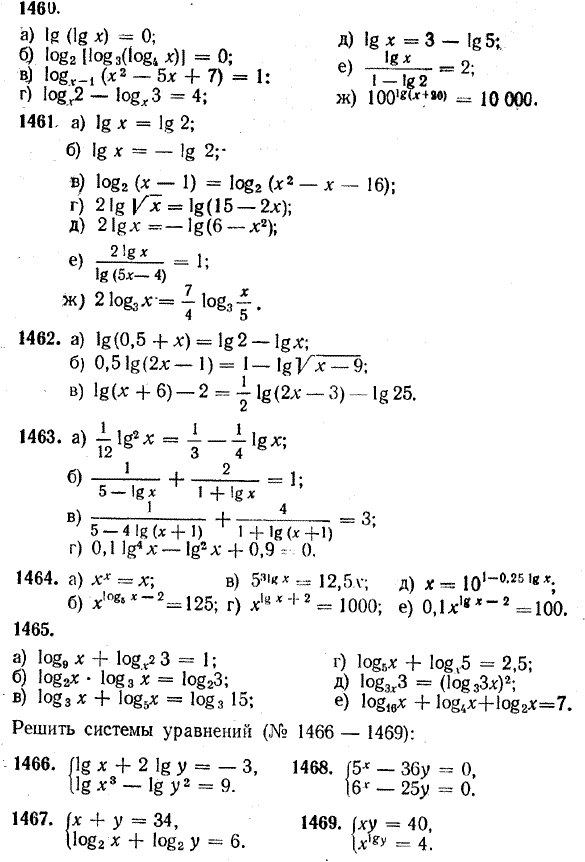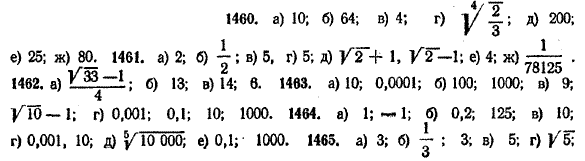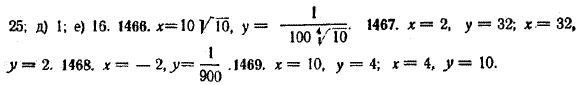ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ   VIII

§ 197. Основные способы решения логарифмических уравнений

Логарифмическими уравнениями называются уравнения, содержащие неизвестные величины под знаком логарифма. К таким относятся, например, уравнения

log₂ x = 5,          log_x (x — 1) = 0

и т. д. Так же как и показательные, логарифмические уравнения являются трансцендентными.

Простейшим логарифмическим уравнением является уравнение

log_a x = b,                                         (1)

где а и b — данные числа, а х — неизвестная величина. Если а — положительное и не равное единице число, то такое уравнение имеет единственный корень

х = а^b.

Решение более сложных логарифмических уравнений, как правило, сводится либо к решению алгебраических уравнений, либо к решению уравнений вида (1). Поясним это на некоторых частных примерах.

I. Решить уравнение

log_x(x² — 3x + 6) =2.

По определению логарифма из этого уравнения следует, что x² = x² — 3x + 6, откуда   х = 2.

Проверка.  При х = 2

log_x(x² — 3x + 6) = log₂ (4 — 6 + 6) = log₂ 4 = 2.

Значит, х = 2 — корень данного уравнения. Ответ,  х = 2.

II. Решить уравнение

lg (x²  —17) = lg (x + 3).

Решение подобных уравнений основано на следующем свойстве логарифмов: если логарифмы двух чисел по одному и тому же основанию равны, то равны и сами эти числа. Из этого свойства логарифмов вытекает, что если только данное уравнение имеет корни, то они должны удовлетворять уравнению

x²  —17 = x + 3,

откуда

x₁ = 5, x₂ = — 4.

Проверка.   При х = 5

lg (x²  —17) = lg 8;    lg (x + 3) = lg 8.

Значит, х = 5 — корень данного уравнения. При х = —4 левая и правая части данного уравнения не определены, поскольку x²— 17=  — 1 < 0 и  x + 3 = — 1 < 0. Следовательно, х = — 4 не есть корень этого уравнения.

Ответ,   х = 5.

Рассмотрим еще одно уравнение

21g (x— 1) = ¹/₂1g x⁵ — lg √x                          (2)

Выполним следующие преобразования:

21g (x— 1) = 1g (x— 1)²,

¹/₂1g x⁵ — lg √x = lg x^5/2  — lg x^1/2  = lg x^5/2/ x^1/2= lg x².

Таким образом, исходя из уравнения (2), мы пришли к уравнению

1g (x— 1)² = lg x².                                  (3)

Из него вытекает, что (x— 1)² = x², или х = ¹/₂.  Но при х = ¹/₂ левая   часть   уравнения   (2)   не   определена (х — 1 = — ¹/₂ <0); следовательно, данное уравнение не имеет корней.

Заметим, однако, что для уравнения (3) число ¹/₂ является корнем.  Таким образом,  уравнения  (2)  и (3)  не   эквивалентны друг другу. Это лишний раз говорит о том,  что  при  решении логарифмических уравнений необходимо делать проверку полученных значений. Среди них часто оказываются «посторонние» корни.

III.  Некоторые логарифмические уравнения сводятся к алгебраическим  уравнениям  посредством  введения   новой   неизвестной величины. Если, например, в уравнении

log₃ ² x — 3log₃  x — 10 = 0

log₃  x   обозначить через у, то оно сведется к  квадратному уравнению у² — 3у — 10 = 0, откуда y₁ = — 2, y₂ = 5.   Вспоминая, что у = log₃  x, получаем: если log₃  x = — 2, то x = ¹/₉; если   же  log₃  x = 5, то х = 243.

Проверкой легко установить, что оба эти значения х  удовлетворяют данному уравнению.

Ответ.   x₁ = ¹/₉  ; x₂ = 243.

IV.  Некоторые уравнения  решаются  путем почленного логарифмирования. Пусть, например, дано уравнение

= 100.

Прологарифмируем это уравнение почленно:

]g  = lg 100,

(lg x— 1) lg x = 2.

Обозначая lg x буквой у,   мы приходим к   квадратному уравнению

у² — у — 2 = 0,

имеющему корни y₁ = — 1, y₂ = 2. Вспоминая, что  у = lg x, получаем: либо lg x = — 1, и тогда х = 0,1; либо lg x = 2, и тогда x =100. Проверка.  При х = 0,1

 = 0,1^—1—1 = 0,1^—2 = ¹/_0,01 = 100;

следовательно, х = 0,1 — корень данного уравнения.

При х = 100

  = 100^2—1 = 100

так что х = 100 — также корень уравнения.

Ответ. x₁= 0,1; x₂ = 100.

V.  При    решении     некоторых    логарифмических   уравнений оказывается полезным использовать формулу перехода от одного основания логарифмов к другому:

Решим, например, уравнение

log₂ x + log₃ x =1.

Для этого от логарифмов по основаниям 2 и 3  перейдем к логарифмам по основанию 10:

log₂ x = ^{lg x}/_{lg2 ,}     log₃ x = ^{lg x}/_{lg3 ,}  

Тогда данное уравнение примет вид:

^{lg x}/_lg2 +  ^{lg x}/_lg3 =1

откуда

При необходимости это значение х можно определить с  помощью таблиц логарифмов.

Проверка.  При найденном значении х

Аналогично,

  log₃ x = ^{lg 2}/_{lg 6}

Поэтому

Значит,   найденное   значение   х   является    корнем   данного уравнения.

Ответ, .

Рассмотрим еще одно уравнение:

log₂ x + log _x 2 = 2

Поскольку

log _x 2 = 1 / log₂ x

то, обозначая log₂ x через у, получаем:

y + ¹/_y = 2,

откуда у = 1. Следовательно, log₂ x = 1 и х = 2. Проверка показывает, что х = 2 есть корень данного уравнения.

О т в е т. х = 2.

Упражнения

Решить данные уравнения  (№ 1460—1465):

ОТВЕТЫ