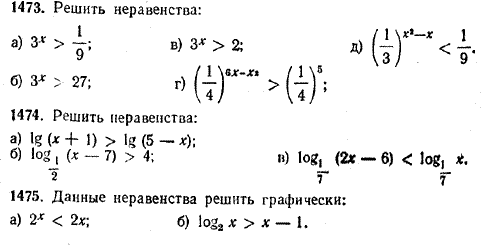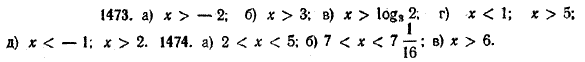ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ   VIII

§ 199. Показательные и логарифмические неравенства

Решение показательных и логарифмических неравенств основано на том, что функции у = а^х и у = log_a x при а > 1 являются монотонно возрастающими, а при 0 < а < 1 — монотонно убывающими.

Рассмотрим   несколько  примеров.

1)  Решить  неравенство

2^х > 4.

Перепишем данное неравенство, представив 4 в виде 2'

2^х > 2².

Функция у = 2^х является монотонно возрастающей. Поэтому большему значению этой функции соответствует большее значение аргумента. Следовательно, х > 2.

2)  Решить  неравенство

 > ¹/₉

Перепишем данное неравенство, представив ¹/₉ в виде 3 ^—2 :

> 3 ^—2

Отсюда     x² — 3x > — 2,    или     x² — 3x + 2 > 0.   Это неравенство выполняется при x < 1, а также при x > 2 (ч. I, § 61).

3) Решить неравенство

log_1/5 (x — l) > — 2.

Представив — 2 как log_1/5 25, перепишем данное неравенство в виде

log_1/5 (x — l) > log_1/5 25.

Функция у = log_1/5 x  является монотонно убывающей.  Поэтому большему значению этой функции соответствует меньшее значение аргумента. Следовательно, х—1 < 25. К этому неравенству необходимо добавить еще неравенство х — 1 > 0, выражающее тот факт, что под знаком логарифма может находиться только положительная величина. Таким образом, данное неравенство эквивалентно системе двух линейных неравенств

х — 1< 25,
х — 1 > 0,

из которой получаем:

1 < х < 26.

Важно отметить, что если бы мы «забыли» учесть условие х — 1 > 0, то пришли бы к неверному выводу: х < 26. В частности, в это «решение» входило бы и значение х = 0, при котором левая часть исходного неравенства не имеет смысла.

Упражнения .

ОТВЕТЫ