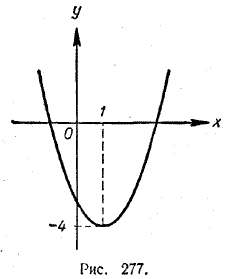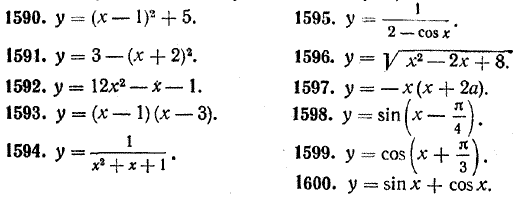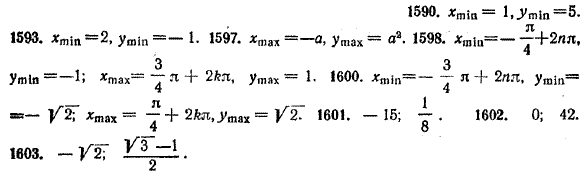|
|
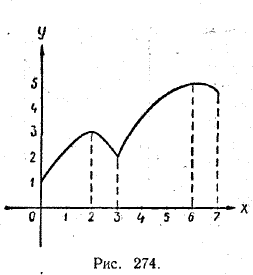
ФУНКЦИИ И ПРЕДЕЛЫ IX § 205. Экстремальные значения функции В этом параграфе мы изучим некоторые вопросы поведения функции у = f (х) в интервале [а, b]. При этом, конечно, мы будем предполагать, что функция f (х) определена в каждой точке этого интервала. Наибольшее из всех тех значений, которые принимает функция у = f (х) в интервале [а, b], называется ее абсолютным максимумом, а наименьшее — абсолютным минимумом в данном интервале. Например, для функции у = f (х) , графически представленной на рисунке 274, абсолютным минимумом в интервале [0,7] является значение f (0) = 1, а абсолютным максимумом — значение f (6) =5.
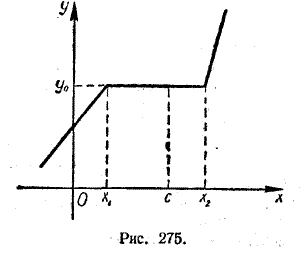
Наряду с абсолютным максимумом и абсолютным минимумом в математике часто говорят о локальных (т. е. местных) максимумах и минимумах. Точка х = с, лежащая внутри интервала [а, b], называется точкой локального максимума функции у = f (х) , если для всех значений х, достаточно близких к с, f (х) < f (с) . (1) Значения функции у = f (х) в точках ее локальных максимумов называются локальными максимумами этой функции. Например, для функции у = f (х), графически представленной на рисунке 274, точками локального максимума являются точки х = 2 и х = 6, а самими локальными максимумами — значения f (2) = 3 и f (6) = 5. В точках х = 2 и х = 6 функция f (х) принимает значения, большие, чем в соседних точках, достаточно близких к ним: f (2) >f (х); f (6) > f (х). Для функции у = f (х), графически представленной на рисунке 275, точкой локального максимума будет, например, точка х = с. Для всех х, достаточно близких к с, f (х) = f (с) , так что условие (1) выполняется.
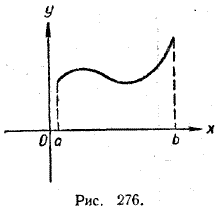
Точка х = x1 также является точкой локального максимума. Для всех значений х, достаточно близких к x1 f (х) < f (x1), если х < x1, и f (х) = f (x1), если х > x1. Следовательно, и в этом случае f (х) < f (x1). А вот точка х = x2 уже не будет точкой локального максимума. Левее ее f (х) = f (x2), но правее ее f (х) > f (x2),. Поэтому условие (1) не выполняется. Точка х = с, лежащая внутри интервала [а, b], называется точкой локального минимума функции у = f (х), если для всех значений х, достаточно близких к с, f (х) > f (с) . (2) Значения функции в точках еe локальных минимумов называются локальными минимумами этой функции. Например, для функции у = f (х), графически представленной на рисунке 274, точкой локального минимума является точка х = 3, а самим локальным минимумом — значение f (3) = 2. Для функции, графически представленной на рисунке 275, точкой локального минимума будет, например, точка х = x2. Для всех значений х, достаточно близких к x2, f (х) = f (x2), если х < x2, и f (х) > f (x2), если х > x2. Следовательно, условие f (х) > f (x2) выполняется. Точка х = с, отмеченная нами выше как точка локального максимума, является вместе с тем и точкой локального минимума. Ведь для всех точек х, достаточно близких к ней, f (х) = f (с), и потому формально неравенство f (х) > f (с) выполняется. Точки минимумов и точки максимумов функции f (х) называются точками экстремумов этой функции. Значения функции f (х) в точках экстремумов называются экстремальными значениями этой функции. Рисунок 274 показывает различие между абсолютными и локальными экстремумами. Функция у = f (х), изображенная на этом рисунке, имеет в точке х = 2 локальный максимум, который не является абсолютным максимумом в интервале [0, 7]. Точно так же и точке х = 3 эта функция имеет локальный минимум, не являющийся абсолютным минимумом в интервале [0, 7]. Если абсолютный максимум функции у = f (х) в интервале [а, b] достигается во внутренней точке этого интервала, то этот абсолютный максимум является, очевидно, и локальным максимумом (см., например, рис. 274 в точке х = 6). Но может случиться, что этот абсолютный максимум достигается не внутри интервала [a, b], а в какой-нибудь крайней его точке (рис. 276).
Тогда он не является локальным максимумом. Отсюда вытекает следующее правило для нахождения абсолютного максимума функции у = f (х) в интервале [a, b], 1. Находим все локальные максимумы функции у = f (х) в данном интервале. 2. К полученным значениям добавляем значения этой функции в концах данного интервала, то есть значения f (а) и f (b). Наибольшее из всех этих значений и даст нам абсолютный максимум функции у = f (х) в интервале [a, b] . Аналогично находится и абсолютный минимум функции у = f (х) в интервале [a, b]. Пример. Найти все локальные экстремумы функции у = x2 — 2х — 3. Каковы наибольшее и наименьшее значения этой функции в интервале [0, 5]? Преобразуем данную функцию, выделив полный квадрат: у = x2 — 2х + 1 —4 = (х — 1)2 — 4. Теперь легко построить ее график. Это будет направленная вверх парабола с вершиной в точке (1, —4) (рис. 277).
Единственной точкой локального экстремума является точка х = 1. В этой точке функция имеет локальный минимум, равный —4. Чтобы найти наибольшее и наименьшее значения данной функции в интервале [0, 5], заметим, что при x = 0 у = — 3, а при х = 5 у = 12. Из трех значений —4, —3 и 12 наименьшим является —4, а наибольшим 12. Таким образом, наименьшее значение (абсолютный минимум) данной функции в интервале [0, 5] равно —4; оно достигается при х = 1. Наибольшее значение (абсолютный максимум) данной функции в интервале [0, 5] равно 12; оно достигается при х = 5. Упражнения 1589. Какие из известных вам функций на всей числовой прямой: а) совсем не имеют локальных экстремумов; б) имеют ровно один локальный экстремум; в) имеют бесконечное множество локальных экстремумов? В упражнениях № 1590—1600 найти точки локальных экстремумов и сами локальные экстремумы данных функций. Выяснить, какие это экстремумы (максимумы или минимумы):
Найти абсолютные экстремумы данных функций в указанных интервалах (№ 1601—1603): 1601. у = — 2x2 — 3x — 1 в интервале | х | < 2. 1602. у = |x2 + 5x + 6| в интервале [— 5, 4]. 1603. у = sin x — cos x в интервале [— π/3 , π/3] 1604. Найти абсолютные экстремумы функции у = (х — 3) (х — 5) в интервалах: а) [2, 3]; в) [4, 5]; б) [3, 4]; г) [2, 5]. ОТВЕТЫ
|