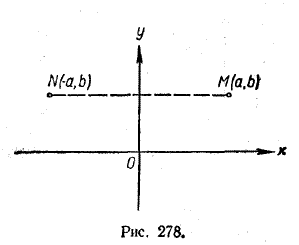
ФУНКЦИИ И ПРЕДЕЛЫ    IX

§ 206. Четные   и   нечетные   функции

Функция у = f (х) называется четной, если при всех значениях х из области определения этой функции

f (— х) = f (х).

Примерами четных функций могут служить хорошо изученные нами функции у = х²,   у = cos х,  у = | х | и т. д.

Пусть точка М с координатами (а, b) принадлежит графику четной функции у = f (х). Тогда b = f (а). Так как функция f (х) четна, то и f (— a)=  f (а)= b. Но это означает, что наряду с точкой М (а, b) графику функции у = f (х)  должна принадлежать и точка N с координатами (— а, b). Эти две точки симметричны друг другу относительно   оси у  (рис. 278).

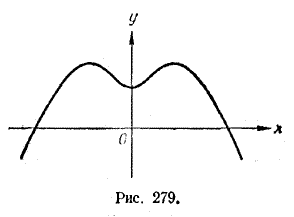
Таким образом, какую бы точку графика четной функции мы ни взяли, на нем обязательно найдется точка, симметричная первой относительно оси у. Вот почему график четной функции представляет собой линию, симметричную относительно оси ординат (один из таких графиков показан на   рис.   279).

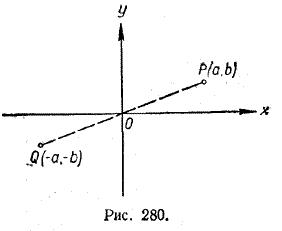
Функция у = f (x) называется нечетной, если при всех значениях х из области определения этой функции

f (— х) = — f (х).

Примерами нечетных функций служат функции у = х,    у = х³,   у = sin х и т. д.

Пусть точка Р с координатами (а, b) принадлежит графику нечетной функции у = f (x); тогда b = f (а). Так как функция f (х) нечетна, то f (— a) = — f (а) .
Поэтому f (— a) = — b. Последнее равенство означает, что точка Q с координатами (— а, — b) должна принадлежать графику функции у = f (x) . Итак, если точка Р с координатами (а, b) принадлежит графику нечетной функции у = f (х), то этому графику должна принадлежать и точка Q с координатами (— а, — b) (рис. 280). Точки Р и Q симметричны относительно начала координат (докажите это!).

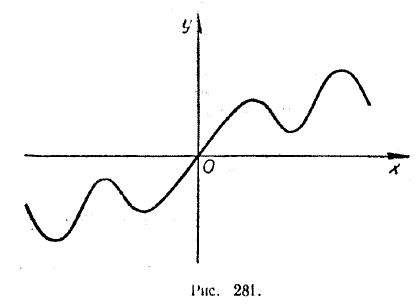
Таким образом, какую бы точку графика нечетной функции мы ни взяли, на нем обязательно найдется другая точка, симметричная первой относительно начала координат. Вот почему график любой нечетной функции симметричен относительно начала координат (см., например, рис. 281).

Не следует думать, что всякая функция является либо четной, либо нечетной. Существует очень много функций, которые нельзя отнести ни к четным, ни к нечетным. Так, например, для функции f (х)  = х + х² имеем: f (— х) = — х + х² . Ни одно из двух тождеств f (— х) = f ( х)  и  f (— х) = — f ( х) не имеет места. Следовательно, данная функция не является ни четной, ни нечетной.

Кроме того, говорить о том, что функция у =  f ( х) четна или нечетна, можно лишь в том случае, когда область определения этой функции является симметричной относительно начала координат. Это означает, что если функция определена при х = а, то она должна быть определена и при х = — а. В противном случае сравнивать выражения f (х)  и  f (— х)  не имеет смысла. Например, функция у = lg х определена только для положительных значений аргумента. Поэтому одно из выражений lg х и lg (— х) наверняка не имеет смысла. Следовательно, говорить о том, является ли логарифмическая функция четной или нечетной, также не имеет смысла.

Упражнения

1605.  (У с т н о.)   Среди   данных функций указать четные и нечетные:

1) y = х¹⁰⁰;                                           8) y =  tg x + ctg x;

2) y = х ^—3;                                           9) y = sin x + cosec x;

3) y = √x ;                                            10) y = x + sin x;

4) y = ³√x;                                          11) y = 2^x+ 2^—x;

5)  y = х⁴ —2х² + 3;                             l2) y =  ^{sin x}/ _x;

6)  y = х³ — 5х —1;                              13) y = ^{cos x}/ _x.

7) y = sin (х²);

1606.   Какие из данных функций являются   четными и какие нечетными:

1) y = 10^—x — 10 ^x;               4) y = sin (х — ^π/₄ );

2)  y = sin (— х);                5) y = sin (х + ^π/₂) ;

3) y = соs (—х);                   6) y = tg (х — ^π/₃)?

1607.  Доказать, что сумма, разность, произведение и частное двух четных функций являются четными функциями.

1608.   Доказать, что произведение и частное   двух нечетных функций представляют собой четные функции.

1609.  Может ли функция быть одновременно и четной и нечетной?

1610*. Что вы можете сказать о четности функции  f ( х), если известно, что функция    |  f ( х) | : а) четна; б) нечетна?

1611. Может ли монотонная на всей числовой прямой функция быть: а) четной; б) нечетной?

1612. Как достроить график четной функции у =  f ( х), еели он задан только при х > 0?

ОТВЕТЫ