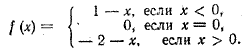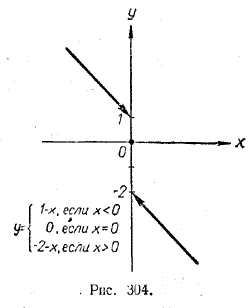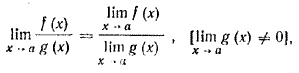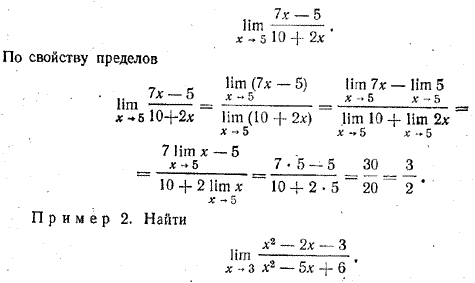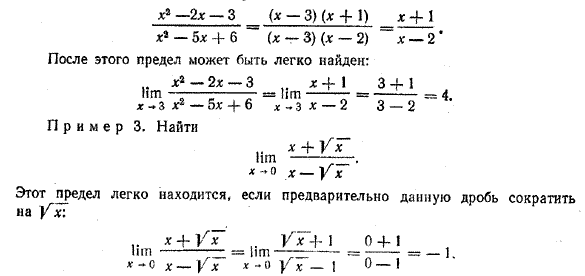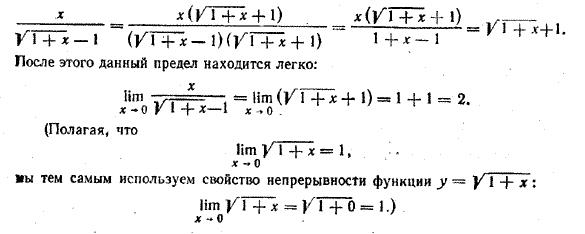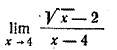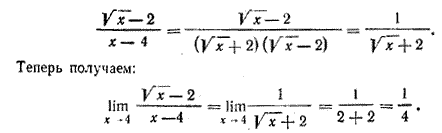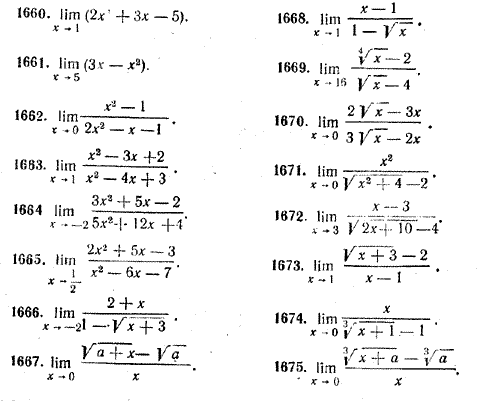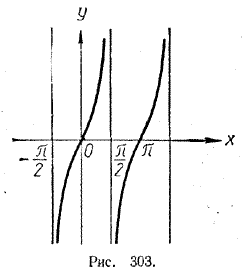
|
|
ФУНКЦИИ И ПРЕДЕЛЫ IX § 212. Основные теоремы о пределах функций Прежде всего заметим, что не для всякой функции у = f (х) существует предел
Поэтому нельзя указать никакого числа b, к которому стремились бы значения этой функции. Другой пример. Пусть
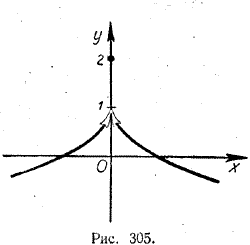
График этой функции представлен на рисунке 304.
Когда значений аргумента х приближаются к 0, оставаясь отрицательными, соответствующие значения функции стремятся к 1. Когда значения аргумента х приближаются к 0, оставаясь положительными, соответствующие значения функции стремятся к —2. В самой же точке х = 0 функция обращается в 0. Очевидно, что указать одно какое-нибудь число, к которому стремились бы все значения у при приближении х к 0, нельзя. Поэтому данная функция не имеет предела при х —> 0. Говоря в дальнейшем о пределе функции, мы всегда будем предполагать, что этот предел существует. Предположение о существовании предела
Очевидно, что предел
Если функция у = f (х) удовлетвoряет условию
то она называется непрерывной в точке х = а. Если же указанное условие не выполняется, то функция f (х) называется разрывной в точке х = а.' Все элементарные функции (например, у = хп, у = sin х, у = tg х , у = tg2 х + tg х и т. д.) непрерывны в каждой точке, в которой они определены. Функция у = f (х) называется непрерывной в интервале [а, b], если она непрерывна в каждой точке этого интервала. Например, функция у = tg x непрерывна в интервале[— π/4 , π/4 ], функции у = sin x и y = cos x непрерывны в любом интервале и т. д. Приведем без доказательства основные теоремы о пределах функций. Эти теоремы вполне аналогичны тем, которые мы рассматривали (также без доказательства) ранее при изучении пределов числовых последовательностей. 1. Предел константы равен самой этой константе:
2. Постоянный множитель можно выносить за знак предела:
3. Предел суммы (разности) функций равен сумме (разности) пределов этих функций:
4. Предел произведения функций равен произведению пределов этих функций:
5. Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:
Рассмотрим несколько типичных примеров нахождения пределов функций. Пример 1. Найти
При х —> 3 числитель и знаменатель данной дроби стремятся к нулю. Поэтому непосредственное применение теоремы о пределе частного здесь невозможно. Однако данную дробь можно сократить:
(Обратите внимание на следующую важную особенность, характерную для рассмотренного примера. Когда мы говорим о пределе Пример 4. Найти
Предел знаменателя дроби при х —> 0 равен 0. Поэтому непосредственное использование теоремы о пределе частного здесь невозможно. Кроме того, данную дробь нельзя сократить, как мы делали это в примерах 2 и 3. В данном случае числитель и знаменатель дроби следует умножить на выражение √1 + х + 1, сопряженное знаменателю дроби. В результате получим:
Пример 5. Найти
При х —> 4 числитель и знаменатель данной дроби стремятся к нулю. Поэтому применить теорему о пределе дроби нельзя. Преобразуем дробь, представив знаменатель в виде произведения:
Упражнения Найти пределы (№ 1660—1675):
ОТВЕТЫ
|
f (х). Так, например, при x —> π/2 значения функции у = tg х (рис. 303) или неограниченно растут (при х < π/2), или неограниченно убывают (при х > π/2). 
f (х) существует и равен 1. Но в самой точке х = 0 функция принимает значение, равное 2. Поэтому в данном случае
определена лишь для положительных значений х. Поэтому, рассматривая предел этой функции, мы фактически предполагаем, что х —> 0, оставаясь все время положительным. В подобных случаях говорят не просто о пределе, а об одностороннем пределе. С аналогичными примерами мы еще встретимся при выполнении упражнений к этому параграфу.)
