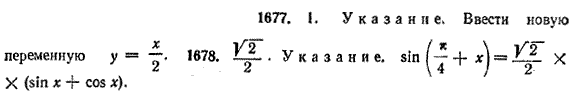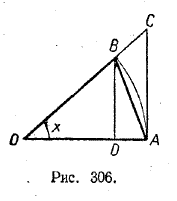
ФУНКЦИИ И ПРЕДЕЛЫ    IX

§ 213. Некоторые тригонометрические неравенства
и их использование при нахождении пределов

В этом параграфе мы докажем некоторые тригонометрические неравенства, которые будут играть важную роль в дальнейшем изучении функций.

1. Для любого острого угла х (выраженного в радианах)

sin х < х < tg x.                          (1)

Доказательство. Пусть на рисунке 306   ОА = ОВ = 1, /   AOB = х радианам, BD и АС перпендикулярны к ОА.

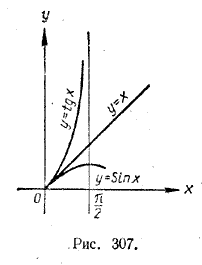
Очевидно, что площадь треугольника ОАВ меньше площади кругового сектора ОАВ, а площадь кругового сектора   ОАВ,   в   свою  очередь,   меньше   площади треугольника ОАС. Но

S_/\ OAB= ¹/₂ OA• BD = ¹/₂ BD;

S_{сект. OAB} = ;

S_/\ OAС = ¹/₂ • OA• АС = ¹/₂ АС.

Учитывая, что BD = sin х, АС = tg x, получаем:

¹/₂ sin х < ^x/₂ < ¹/₂ tg x

откуда и вытекает неравенство (1).

Рисунок 307 служит графической иллюстрацией неравенства (1).

В интервале (0, ^π/₂) график функции у = х расположен выше  графика функции у = sin х, но  н и ж е   графика функции у = tg x.

Остановимся подробнее на неравенстве sin x < х. Мы доказали его в предположении, что 0 < х < ^π/₂. Но при таком предположении х и sin x положительны. Поэтому х = |х| и sin х = |sin х| и неравенство sin х < х можно переписать в виде:

|sin х| < | х |.                                     (2)

Это неравенство верно и для отрицательных значений х, заключенных в интервале (—^π/₂, 0), так как

| sin ( — х)| = | — sin х| = | sin х |,

Перепишем неравенство (2) в виде:

| sin х — 0| < | х |.

Если х стремится к 0, то |sin х — 0|, будучи меньше | х |, тем более будет стремиться к нулю. В частности, |sin х — 0|   может стать меньше 0,1; 0,01; 0,001 и т. д. Вообще, какое бы малое положительное число ε мы ни взяли, всегда можно добиться, чтобы выполнялось неравенство |sin х — 0| < ε. Для этого нужно х выбирать в интервале (— ε, ε). Но это означает, что

sin x = 0.

Предел  синуса х   при   х —> 0   равен  0.

(Поскольку 0 = sin 0, то полученный результат по существу означает, что функция у = sin x непрерывна в нуле (то есть при х = 0.)

2. Для любого острого угла х (выраженного в радианах)

1 — cos х < х.                        (3)

Действительно,       1 — cos x = 2sin^{2 x}/₂ .           

Но  0 < sin ^x/₂ < 1. Поэтому sin^{2 x}/₂  < sin ^x/₂. По доказанному выше sin ^x/₂ < ^x/₂ 

Итак,

1 — cos х = 2sin^{2 x}/₂ < 2sin ^x/₂ < 2 ^x/₂ = х,

что и доказывает формулу (3).

Если угол х острый, то х и 1 — cos х  положительны.
Поэтому х = |х| , 1 — cos х = |1—cos x |. Следовательно, неравенство (3) можно переписать в виде:

|1—cos x | <  |х|.                 (4)

Это неравенство, очевидно, верно и при х < 0, поскольку

|1 — cos(— х)| = |1 — cos х|;    |— х| = | х |.

Из (4) вытекает, что

cos x = 1

Предел косинуса  х  при   х —> 0   равен 1.

Поскольку   1 = cos 0,  то  полученный  результат  по существу  означает, что  функция у = cos х непрерывна в нуле.

Отсюда, используя доказанную выше непрерывность в нуле функции у =  sin х, легко показать, что функции у = sin х  и  у = cos x  непрерывны в любой  точке х. Попробуйте это сделать сами!

Упражнения

Найти пределы (№ 1676 —1681):

1676. tg х.               1678.  sin ( ^π/₄ + х).         1680.  tg ( ^π/₃ +2х).

1677.    cos ^x/₂.        1679.  sin 2х.                    1681.  cos ( ^π/₃ — х ).

1682.  Доказать тождества:

a)   sin (х + α) = sin α;            6)  cos (х + α) = cos α.

1683.  Для всех ли положительных значений х верны неравенства:

а) sin х < х;                    б) х < tg x?

1684.  Докажите,  что единственным корнем  уравнения sin х = х является х = 0.

ОТВЕТЫ