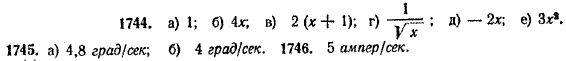ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ  X

§ 219. Производная   функции.

На протяжении всего школьного курса алгебры и элементарных функций мы расширяли математические понятия, углубляли их, доводя до более общих, более сложных понятий. То же самое нам предстоит сделать и в этом параграфе.

Что представляет собой мгновенная скорость движения, определенная в § 218?

Имеется некоторая функция s (t), указывающая путь, пройденный телом за время от 0 до t. Аргументу t дается некоторое приращение τ, то есть вместо значения t рассматривается значение t + τ. Этому приращению аргумента соответствует следующее приращение функции  s (t):

s (t + τ) — s (t).

Это приращение функции делится на приращение аргумента τ

s (t + τ) — s (t)
τ

и берется предел при τ —> 0. Выражение

s (t + τ) — s (t)
τ

можно рассматривать как «среднюю скорость» измейения функции s (t) в интервале от t до t + τ, а предел этого отношения при τ —> 0 — как мгновенную скорость изменения этой функции в момент времени t.

В приведенных выше рассуждениях функция s (t) представляла собой путь, пройденный телом за время от 0 до t. Это обстоятельство накладывало на функцию s (t) определенные ограничения. В частности, она должна была быть определена только для неотрицательных значений аргумента t (ведь t — время), принимать только неотрицательные значения (s — длина пути) и быть монотонно возрастающей (чем больше время, тем больше пройденный путь). Теперь же мы обобщим наши результаты на произвольные функции, вообще говоря, никак не связанные с движением тел.

Пусть f (х) — произвольная функция. При фиксированном значении x₀ аргумента х эта функция принимает значение, равное f (х₀). Дадим значению x₀ приращение Δx₀*, то есть вместо значения x₀ рассмотрим значение x₀ + Δx₀. Тогда функция  f (х) примет значение f (x₀ + Δx₀) и, таким образом, получит приращение Δy₀**:

Δy₀ = f (x₀ + Δx₀) — f (х₀)

* Выражение Δx₀ читается: дельта икс нуль. Это одно, нераздельное выражение. Его не следует путать с произведением Δ • x₀.

** Δy₀ также нераздельное выражение. Его не следует путать с произведением Δ • y₀.

Отношение

представляет собой среднюю скорость изменения функции  f (х) в интервале от х₀ до кx₀ + Δx₀. Эта средняя скорость зависит, очевидно, как от х₀, так и от Δx₀ . Устремляя теперь Δx₀  к нулю, мы получим мгновенную скорость изменения функции  f (х) в точке х = x₀:

(если, конечно, указанный предел существует). Для заданной функции f (х) этот предел зависит от x₀ и называется производной от функции f (х) в точке х = x₀. Каждому значению x₀ соответствует свое значение мгновенной скорости изменения функции f (х). Поэтому предел (если только он существует)

представляющий собой мгновенную скорость изменения функции f (х) в произвольной точке х, можно рассматривать как новую функцию аргумента х. Эта новая функция называется производной от заданной функции f (х).

Часто в выражении «производная от функции f (х)» слово «от» опускают и говорят просто «прoизводная функции f (х)».

В математике используется несколько обозначений производной. Мы будем пользоваться следующими обозначениями: у' и f '(х):

Рассмотрим несколько примеров.

Пример 1. Найти производную функции f (х) = с, где с = некоторая константа.

Имеем: f (х) = с,   f (х + Δx) = с.

Поэтому   Δy =  f (х + Δx)  — f (х)  = с — с = 0   и,    следовательно,   

^Δy/_Δx  = ⁰/_Δx = 0

Таким образом,

y'  = ^Δy/_Δx = 0 = 0

Производная константы равна 0.

Пример   2.   Найти производную функции f (х) = х.

Имеем:

f (х) = х,  f (х + Δx) = х + Δx.

Поэтому

Δy =  f (х + Δx)  — f (х)  = (х + Δx) — х = Δx.

Следовательно,

^Δy/_Δx  = ^Δx/_Δx  = 1

Отсюда вытекает, что :

y'  = ^Δy/_Δx = 1 = 1

Производная от функции  f (х) = х  равна 1.

Пример   3.   Найти производную функции f (х) = х².

Имеем:

f (х) = х²,   f (х + Δx)  = (х + Δx)².

Поэтому

Δy =  f (х + Δx)  — f (х)  =  (х + Δx)² — х² = [х² + 2х • Δx + (Δx)²] — х² = 2х • Δx + (Δx)²

Значит,

^Δy/_Δx = 2х + Δx

Следовательно,

y'  = ^Δy/_Δx = ( 2х + Δx ) = 2х + Δx = 2х + 0 = 2х

Производная от функции   f (х) = х²  равна  2х.

В отличие от первых двух примеров здесь производная зависит  от х.

Значение производной от функции  f (х)  при х = а обозначают f '(a).

Например, если f (х) = х², то f '(х)  = 2х и потому

f '(0) = 2 • 0 = 0.

f '(1) = 2 • 1 = 2.

Упражнения

1744.  Найти производные следующих функций:

а) у = х + 1;              в) у = (х + 1)²;              д) у = 1 — х²;

б) у = 2х²;                г) у = 2√x;                      е)  у = х³.

1745.  При нагревании тела его температура Т изменяется с течением времени t по закону Т = 0,4t ² (T — температура в градусах, t — время в секундах). Найти:

а)  среднюю скорость изменения температуры тела за промежуток времени от t₁ = 4 сек до t₂ = 8 сек;

б)  мгновенную скорость изменения температуры тела в момент  t = 5 сек.

1746.  Ток I ампер изменяется с течением времени  t по закону I = 0,5t ², где t — число секунд. Найти скорость изменения  тока в конце  пятой секунды.

ОТВЕТЫ