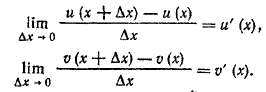ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ  X

§ 224. Производная суммы функций

Теорема. Если функции u (x) и v (x) дифференцируемы, то их сумма
w (x) = и (x) + v (x) также дифференцируема, причем

w' (x) = и' (x) + v' (x)

(Производная от суммы двух функций равна сумме производных от этих функций.)

Доказательство.  Имеем:

Δ w (x)  = w (x + Δ x) — w (x) = [и (x + Δ x) + v (x + Δ x)] — [и (x) + v (x)] =

= [и (x + Δ x) — и (x)] +   [v (x + Δ x) — v (x)].

Поэтому

Так  как функции  u (x) и v (x)  дифференцируемы,  то   существуют   пределы

Следовательно, существует и предел

 ^Δw/_Δx= w' (x)

причем

w' (x) = и' (x) + v' (x)

Мы получили формулу для производной суммы двух функций. Аналогично можно получить и формулу для производной разности двух функций

 [и (x) — v (x)]' = и' (x) — v' (x).

Впрочем, ее можно вывести из формулы для производной от суммы, если выражение и (x) — v (x) рассматривать как сумму и (x) + [ — v (x) ] и использовать теорему о вынесении постоянного множителя за знак производной. Предлагаем учащимся разобраться в этом самостоятельно.

Отметим, что доказанная выше теорема верна для любого конечного числа слагаемых:

(u₁ + u₂ + ... + u_n )' = u'₁ + u'₂ + ... + u'_n .

Примеры.   Пусть f (x) = x² + 2х — 5.

Тогда

f '(x) = (x²)' + (2х)' — (5)'   =   2х + 2 — 0 = 2х + 2.

Аналогично,

( — 3x²  + 5х + 7)' = (—3x²)' + (5х)' + (7)'= — 3 • 2х + 5 • 1 + 0 = — 6х + 5.

Упражнения

Найти  производные  следующих функций:

1756. (Устно.) .

а) у = 1— х ;                      г) у =1 — 3х + 6x²;         ж) у = х (1 — х);

б) у = х — x²                     д) у = 6 — 3x²;                з) у = (х + 1)(х — 1).

в) у = 2х + x² — 7;            е) у = х — ^√2/₂ x²;

1757. у = (х — 1 ) (х + 2).                   1760. у = (3 — 2х) (х — 6).

1758. у = (х — 1)².                              1761. у = 3х — 5 (1 — х) (1 — 2х).

1759. у = (2х — 1)².                            1762. у = (х — 1)² — (х + 1)².

ОТВЕТЫ