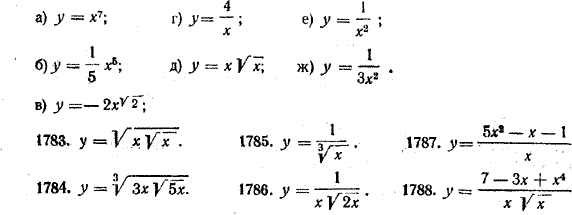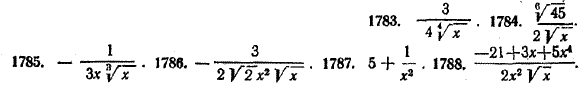ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ  X

§ 227. Производная степенной функции

В предыдущих параграфах мы уже рассматривали некоторые примеры на нахождение производной от степенной функции у = хⁿ при натуральном п. Так, например, мы доказали, что (х)' = 1, (x²)' = 2х. Используя теорему о производной произведения двух функций, легко получить производные и любых других натуральных степеней х. Например,

(x³)' = (x² • х)' = (x²)' •  х + x² •  (х)' = 2х •  х + x² • 1 = 3x²;

(x⁴)' = (x³ •  х)' = (x³)' •  х + x³ •  (х)' = 3x² • х + x³ •  1 = 4x³;

(x⁵)'= (x⁴ • х)' = (x⁴)' • х + x⁴ • (х)' = 4x³ • х + x⁴ •  1 = 5x⁴

и т. д. Нетрудно подметить общее правило для нахождения производной от функции  у = хⁿ при любом натуральном п.

Чтобы найти производную функции у = хⁿ, нужно показатель п взять коэффициентом., а у самого х показатель понизить на единицу, то есть

(хⁿ)' = пх^n—1.           (1)

Например,

(x¹⁰)'= 10x⁹,           (x⁴⁵)'= 45x⁴⁴

Рассуждения, которые мы проводили здесь в подтверждение справедливости формулы (1), являются лишь наводящими; за строгое доказательство этой формулы их принять, конечно, нельзя. К формуле (1) мы еще вернемся в § 262 где и дадим ее строгое доказательство.

Полученное нами правило нахождения производной от степенной функции верно не только для натуральных, но и для любых показателей, то есть для любого действительного числа α

(х^α)' = αх^α—1 (х > 0).

Доказательство этой формулы выходит за пределы школьной программы и поэтому здесь не приводится.

Примеры:

1) Пусть у = ¹/_x. Тогда

у' = (¹/_x)' = (х^—1) = — 1 • х^—1—1 = — х^—2 = — 1/х²    ( x =/= 0).

2)  Пусть у = √x. Тогда

у' = ( √x )' = ( x ^½ )' = ¹/₂ x ^{½ —1} = ¹/₂ x ^{— ½} = ¹/_2√x   ( x > 0)

3)  При у = ¹/_√x

у' = ( ¹/_√x )' = ( x ^—½ )' = —¹/₂ x ^{—½ —1} = —¹/₂ x ^{— 3/2} = — ¹/_2x√x   ( x > 0)

Упражнения

Найти производные следующих функций (№ 1782-4788):

1782. (У с т н о.)

1789. Почему, приводя общую формулу    (х^α)' = αх^α—1

обычно оговаривают, что х > 0?

ОТВЕТЫ