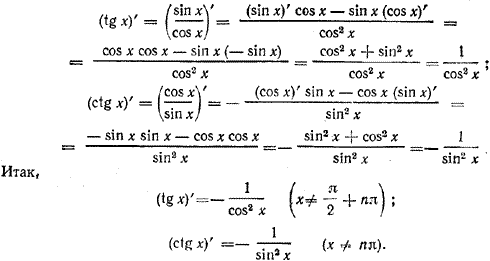|
|
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ X § 229. Дифференцирование тригонометрических функций Теорема 1. Производная синуса равна косинусу: (sin x)'= cos x. Доказательство. Пусть аргумент х получил приращение Δх. Тогда функция у = sin х получит приращение Δy = sin (х + Δх) — sin x. Преобразуем это выражение, используя формулу для синуса суммы двух углов: Δy = sin х • cos (Δх) + cos х • sin (Δх) — sin x = cos х • sin (Δх) — sin x (1 — cos Δх). Учитывая, что 1 — cos Δх = 2 sin2 ( Δ x/2 ), получаем: Δy = cos x sin Δх — 2 sin x sin2 ( Δ x/2 ). Отсюда Δy/Δx = cos х • sin
Δx/Δ x — 2 sin x • Мы знаем (гл. IX, § 214), что
Следовательно, Теперь из (1) получаем: (sin x)' = = cos х • 1 — 2 sin х • 0 = cos x. Теорема доказана. Теорема 2. Производная косинуса равна синусу, взятому с противоположным знаком: (cos х)' = — sin х. Доказательство. Пусть аргумент х получил приращение Δх. Тогда функция у = cos х получит приращение Δy = cos (х + Δх) — cos х. Преобразуем это выражение, используя формулу для косинуса суммы двух углов: Δy = cos (х + Δх) — cos x = cos x • cos Δх — sin x sin Δх — cos x = = — sin x sin Δх — cos x (1 — cos Δх) = — sin x sin Δх — 2 cos x sin2 ( Δ x/2 ). Отсюда Δy/Δx = — sin x sin
Δx/Δ x — 2 cos x но
Поэтому (cos x)' = Теорема доказана. Примеры. 1) Найти производную функции у = a sin x + b cos x. Имеем: y' = (a sin x + b cos x)'= а (sin x)' + b (cos x)' = a cos x — b sin x. 2) Найти производную функции у = x sin x. По правилу дифференцирования произведения двух функций получаем! y' = (x sin x)' = x' sin x + x (sin x)' = sin x + x cos x. Используя правило дифференцирования дроби, легко найти производные функций tg х при х =/= π/2 + пπ и ctg х при х =/= пπ. Действительно,
Упражнения 1797. Написать уравнение касательной к синусоиде у = sin x в точке с абсциссой: а) х = 0; б) х = π/2; в) х = 3/2 π; г) х = π/4; д) х = π. 1798. Написать уравнение касательной к косинусоиде у = cos x в точке а абсциссой: а) х = 0; б) х = π/2; в) х = 3/2 π; г) х = π/4; д) х = π. Найти производные следующих функций: 1799. у = 3 sin х + 2 cos х. 1805. у = sin х • cos х. 1800. у = 4 sin х — 5 cos х. 1806. у = х2 sin х. 1801. у = — sin х + 7 cos х. 1807. у = х2 cos х. 1802. у = — 6 sin х — 9 cos х. 1808* у = cos2 x/2 . 1803. у = sin2 х. 1809. у = (5х + sin х) (х2 — cos х). 1804. у = cos2 х. 1810. у = (1 — 2 sin х) (1 — 3 cos х).
1811. у = sin 2х. 1812. у = cos 2х. 1817. у = 3cos х/ √x 1813. у = (a + bх) sin х + (c + dх) cos х. 1814. у = sin x/ x . 1818. у = sin (х + π/4) . 1815. у = sin2 х + cos2 х. 1816. у = √x sin х 1819. у = cos (х — π/3). ОТВЕТЫ
|
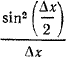 (1)
(1)