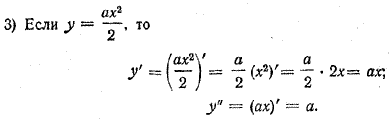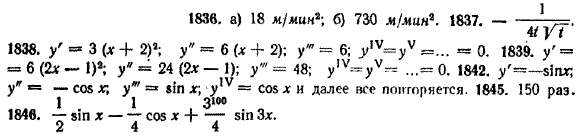ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ  X

§ 231. Понятие о второй производной. Производные высших порядков

Производная от производной у' функции у называется второй производной этой   функции и обозначается у" или f"(х):

y" = (y')';     f"(х) = [ f(х)]'.

Рассмотрим несколько примеров.

1)  Пусть      у = 3x³ — 6x² + 7х — 1.

По правилу дифференцирования многочленов

у' = (3x³ — 6x² + 7х — 1)' = 9x² — 12x + 7;

y"  = (у')' = (9x² — 12x + 7)' = 18x — 12.

2)  Пусть    у = sin х. Тогда

у' = (sin х)' = cos х;         y"  = (cos х)' = — sin x.

Вторая производная y" функции y, так же как и первая ее производная у', допускает простую физическую интерпретацию. Будучи производной от первой производной у', она характеризует скорость изменения этой производной. Первая же производная у' характеризует скорость изменения функции у. Таким образом, у" характеризует «скорость изменения скорости изменения» функции у. С подобным понятием мы уже сталкивались в физике. Изучая равноускоренное движение, мы вводили понятие ускорения как изменения скорости движения в единицу времени. Это понятие как раз и характеризует скорость изменения скорости движения. Поэтому, используя язык механики, можно сказать, что вторая производная у" функции у есть ускорение, с которым функция
у = f (х) изменяет свои значения при изменении значений аргумента х.

Третья производная функции у = f (х) есть производная от второй производной этой функции. Она обозначается у"' или f'"'(x) :   у'" = (у")',  f'"'(x) =  [f'"(x)]'. Аналогично, четвертая производная функции у = f (х)  обозначается  y^IV или  f' ^IVx)  есть производная от ее третьей производной и т. д.

п-я производная функции  f (х) иначе называется производной п-го порядка (обозначается f ⁿ(х)). Например, третья производная иначе называется производной третьего порядка, четвертая производная — производной четвертого порядка и т. д.

Примеры.

1)  Для функции у = x² + х + 1 имеем:

у' = 2х+ 1;

у" = 2;

 y''' = 0

  y^IV  = 0.

Очевидно, что все производные данной функции, начиная с третьей, равны нулю.

2)  Для функции у = sin x:

у'   = cos x;

у" = — sin x;

y'''  = — cos x;

y^IV = — ( — sin x) = sin x;

y^V  = cos x      и т. д.

Упражнения

1836.  Найти ускорение тела, движущегося по закону s (t) = 2t³ + 5t² + 4t (s — путь в метрах, t — время в минутах), в момент времени:    a) t = 40 сек;      б) t = 1 ч.

1837.  Найти ускорение тела, движущегося по закону s = √t (s — путь   в метрах, t — время в минутах), в произвольный момент времени t.

Для данных функций найти производные всех порядков (1838—1843):.

1838.  у = (х + 2)³.          1840. у = х² — х— 1.             1842. у = cos х.

1839.  у = (2х — 1)³.        1841. у = х⁵+ 4х³ — 7х²        1843. у = (1 + х)¹⁰⁰.

1844. Доказать,  что для функции у = a sin x + b cos х справедливо соотношение y^IV= у.

1845.  Сколько раз нужно продифференцировать функцию  у = (х² + 1)¹⁰⁰, чтобы в результате получился многочлен 50-й степени?

1846*. Найти производную 100-го порядка от функции у = sin х cos²х.

ОТВЕТЫ