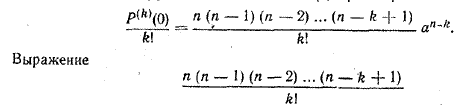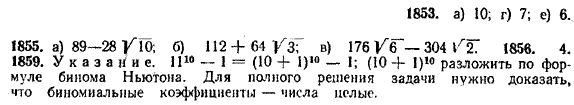ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ  X

§ 233. Формула бинома Ньютона

До сих пор нам были известны формулы для второй и третьей степени двучлена a+b:

(a+b)² = а² + 2аb + b²,

(a+b)³ = а³ + 3а²b + 3ab² + b³.

В этом параграфе мы получим формулу для степени (а + b)ⁿ с произвольным натуральным показателем п. Для этого рассмотрим многочлен степени п

Р (х) = (х + а)ⁿ,

где а — некоторое заданное число.

Свободный член этого многочлена равен Р (0) = аⁿ. Для нахождения коэффициентов при степенях х воспользуемся формулой (6) предыдущего параграфа.

Согласно этой формуле коэффициент при x^k равен , где Р^k (0)—значение k-й производной многочлена Р (х) при х = 0. Найдем это значение. Имеем:

Р (х) =(х+ а)ⁿ;

Р' (х) = п (х + а)^{п— 1};

Р" (х) = п (п — 1) (х + а)^{п— 2};

Р'" (x) =  п (п — 1) (п — 2) (х + а)^{п— 3}

и т. д. Очевидно, что k-я производная многочлена Р (х) равна:

Р^k (х) = п (п — 1) (п — 2) ... (п — k + 1) (х + а)^{п— k}.

Поэтому

Р^k (0) = п (п — 1) (п — 2) ... (п — k + 1) а^{п— k}.

Следовательно, коэффициент многочлена Р (х) при x^k равен:

принято обозначать C_n^k (читается: це из эн по ка). Поэтому коэффициент многочлена Р (х) при x^k равен C_n^k а^{п— k}. Например, коэффициент при х равен C_n¹ а^{п— 1}, коэффициент при x² равен C_n² а^{п— 2} и т. д. Но в таком случае данный многочлен можно представить в виде:

(х + а)ⁿ = а^п + C_n¹ а^{п— 1} х + C_n² а^{п— 2} x² + ... + C_n^{п— 1} ах^{п— 1} + C_n^п х^п.

Полагая в этой формуле х = b, получим:

(a + b)ⁿ = а^п + C_n¹ а^{п— 1} b + C_n² а^{п— 2} b² + ... + C_n^{п— 1} аb^{п— 1} + C_n^п b^п      (1)

Отметим, что (k + 1)-е по счету слагаемое в разложении (a + b)ⁿ имеет вид:

C_n^kа^{п— k} b^k        (0 < k < п).

Формула (1) называется формулой бинома* Ньютона, а коэффициенты 1, C_n¹, C_n² , ... , C_n^{п— 1} , C_n^п, участвуют в ней, — биномиальными коэффициентами.

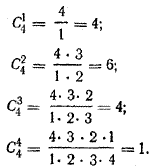
* Формула (1) была строго доказана еще до Ньютона Якобом Бернулли (1654—1705)—одним из членов семьи швейцарских ученых, давшей миру 11 видных математиков. Ньютону принадлежит идея о распространении формулы (1) на случай дробных и отрицательных значений n. Эта идея широко используется при решении многих задач высшей математики.

Пример.

(a+b)⁴  = а⁴ + C₄¹ а³b + C₄² а²b² + C₄³аb³ + C₄⁴b⁴.

Но

Поэтому

(a+b)⁴ = а⁴ + 4 а³b + 6 а²b² + 4 аb³ +  b⁴.

Упражнения

1853.   Вычислить:

а)   C₅²;    б) C₆³;        в) C₈³;        г) C₇⁶;        д) C₁₀⁴;        e) C₆⁵

1854.  Исходя из формулы бинома Ньютона, тюлучить формулы для кубов суммы и разности двух чисел.

1855.   Вычислить по формуле бинома Ньютона:

а) (√5 — √2 )⁴;    б) (√6 + √2 )⁴; в) (√6 — √2)⁵;   г) (√10 — √2)⁵.

1856.  Определить степень бинома (3а — 2)^п, если известно, что коэффициент при а² в разложении этого бинома равен 216.

1857.  Доказать равенства:

а) C_n^{п— 1}  = C_n¹ = n ;        б)  C_n^{п— 2}  = C_n² = 

1858.  Доказать тождество:

1859*. Доказать, что число 11¹⁰ — 1 делится на 100.

ОТВЕТЫ