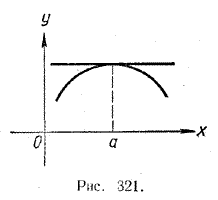
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ  X

§ 237. Применение производной к нахождению локальных экстремумов функции

В этом параграфе мы покажем, как с помощью производной можно находить локальные экстремумы дифференцируемой функции.

Теорема. Если точка х = а является точкой локального экстремума дифференцируемой функции y= f (x), то производная f'(x) в этой точке обращается в нуль:

f '(a) = 0.

Доказательство этой теоремы выходит за пределы школьной программы, поэтому мы ограничимся лишь  ее геометрической  иллюстрацией.

Пусть точка х = а является точкой локального максимума функции y= f (x) (рис. 321).

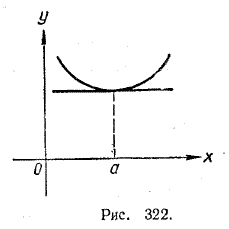
Тогда касательная к графику этой функции в точке с абсциссой a будет параллельна оси х. Угловой коэффициент этой касательной равен 0. Но, как мы знаем, этот угловой коэффициент должен равняться f '(a) . Следовательно,

f '(a) = 0.

Аналогично интерпретируется случай, когда точка х = а является точкой локального минимума (рис. 322).

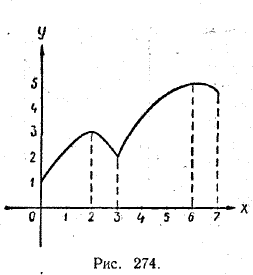
Важно подчеркнуть, что полученное условие f '(a) = 0 относится лишь к функциям, дифференцируемым в точке х = а. Вообще же функция может иметь локальный экстремум в точке х = а и будучи недифференцируемой в этой точке. Взгляните, например, еще раз на кривую, представленную на рисунке 274 .

Эта кривая служит графиком функции f (x), для которой точка х = 3 является точкой локального минимума. Но эта функция при х = 3 не имеет производной (кривая в точке с абсциссой 3 не имеет касательной). Поэтому условие f '(3) = 0 не выполняется.

Пример.   Функция f (x) = ax²  + bx + c имеет единственный локальный экстремум в точке х = —  ^b/_2a. В этом легко убедиться путем выделения из данного квадратного трехчлена полного квадрата (см. ч. I, § 49):

Легко проверить,  что f '(—  ^b/_2a) = 0.

Действительно, поскольку f (x) = ax²  + bx + c,   то

f ' (x) = 2ах+ b

и потому

f '(—  ^b/_2a) = 0

Естественно возникает вопрос: как, зная, что х = а есть точка локального экстремума функции  f (x) , определить, какой экстремум она дает: максимум или минимум?

Пусть при х < а  f ' (x) < 0, а при х > a  f ' (x) > 0. Тогда вблизи точки х = а функция f (x)  должна убывать в точках, лежащих левее а, и возрастать в точках, лежащих правее а (рис. 322). В этом случае точка х = а является точкой локального минимума. Если же при х < a     f ' (x) > 0, а при х > a    f ' (x) <  0, то, наоборот, левее точки х = а функция   f  (x) будет возрастать, а правее х = а убывать. В этом случае точка х = а будет точкой локального максимума (рис. 321).

Итак, если производная  f ' (x) в точке х = а обращается в нуль, а при переходе через эту точку меняет свой знак с «—» на  «+» , то точка а есть точка локального минимума функции  f '(x).

Если производная f ' (x) в точке х = а обращается в нуль, а при переходе через эту точку меняет свой знак с «+» на «—», то точка а есть точка локального максимума функции f (x).

Например, для функции  f (x) = ax²  + bx + c    производная f ' (x) = 2ах+ b  обращается в нуль  при х =  —  ^b/_2a. Предположим,  что   а > 0;   тогда   при   х < —  ^b/_2a получим:

2ах < — b,

2ах + b < 0

а при х > —  ^b/_2a

2ах > — b,

2ах + b > 0

Итак, если а > 0, то при переходе через точку  х =  —  ^b/_2a производная  функции   f (x) = ax²  + bx + c  меняет знак с «—» на «+». Поэтому точка  х =  —  ^b/_2a  является точкой локального   минимума  этой функции.  К такому же результату мы приходили  и раньше, рассматривая выражение

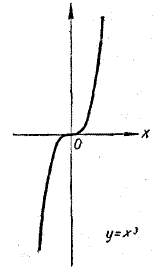
Учащимся предлагается самостоятельно с помощью производной рассмотреть случай, когда а < 0, и убедиться, что   тогда   точка  х = ^b/_2a является   точкой локального максимума функции   f (x) = ax²  + bx + c.

Не следует думать, что если f '(a) = 0, то точка х = а обязательно является точкой локального экстремума. Например, для функции    f (x) = x³    имеем   f '(x) = 3x², и поэтому  f '(0) = 0. Но, как видно из графика этой функции (рис. 323), точка х = 0 не является ни точкой локального минимума, ни точкой локального максимума. Объясняется это тем, что в точке х = 0 производная  f '(x) = 3x², обращаясь в нуль, не меняет своего знака. Как при х < 0, так и при х > 0 она положительна.

Можно доказать, что

если f '(a) = 0 и при переходе через точку х = а производная  f '(x)  не меняет знака («+» переходит в «+» или « — » в « — »), то точка х = а не является ни точкой локального минимума, ни точкой локального максимума.

Точки, в которых производная  f '(x) функции  f (x) обращается в нуль, называются стационарными точками, а значения функции в этих точках — стационарными значениями этой функции.

Упражнения

Для данных функций (№ 1898—1909) найти все локальные экстремумы. По возможности выяснить, какие из них представляют собой локальные минимумы и какие — локальные максимумы:

1898.  у = 4x² — 6x — 7.                                  1903.  у = 2x³— 6x²— 48x —17.

1899.  у = — 3x² — 12x + 100.                        1904. у = 3x⁴ — 4x³.

1900.  у = (а — х) (а — 2х).                            1905. у = sin x + cos x.

1901.  у = (1 — аx) (1 — 2x).                          1906. у = √3 sin x — cos x.

1902.  у = 2x³ + 6x² — 18x + 120.                   1907. у = sin х +  √3 cos х.

1908. у = x⁵.                      

1909. у = sin² х — cos² х.

В задачах № 1910—1913 найти  стационарные  значения  данных функций:

1910.  у = х — sin х + cos х                  1912. у = 5 sin х + 12 cos х — 13х.

1911.   у = 2х + sin х — √3 cos х.            1913. у = sin² х — cos х.

1914.  Докажите, что функция f (х) = | х |  имеет в точке х = 0 локальный минимум. Удовлетворяется ли при этом условие f '(0) = 0?

1915.  В конус вписан цилиндр наибольшего объема. Докажите, что радиус этого цилиндра составляет ²/₃ радиуса основания конуса, а высота — ¹/₃ высоты конуса.

ОТВЕТЫ