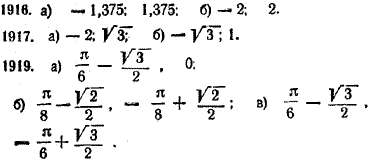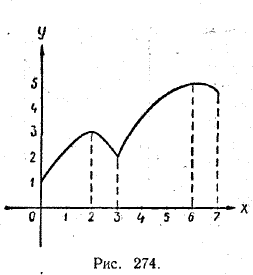
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ  X

§ 238. Наименьшее и наибольшее значения функции в заданном интервале

В главе IX (§ 205) мы рассмотрели вопрос о том, как отыскивается абсолютный минимум и абсолютный максимум функции f (х) в интервале [а, b]. Среди всех локальных экстремумов и значений функции f (х)  в концах интервала [а, b] нужно выбрать наименьшее и наибольшее значения. Они и дают абсолютные экстремумы. Однако в главе IX мы не могли решить вопрос о том, как находить локальные экстремумы. Теперь же мы можем решить эту задачу.

Для того чтобы найти абсолютный минимум и абсолютный максимум дифференцируемой функции  у = f (х)  в интервале [а, b], нужно:

1)  из уравнения f '(х) = 0 найти все стационарные точки функции f (х) и, выбирая те из них, которые попадают в интервал [а, b], определить стационарные значения этой функции в данном интервале;

2)  к стационарным значениям функции f (х)  в интервале  [а, b] добавить значения этой функции в концах этого интервала, то есть f (a) и f (b); среди полученных значений нужно выбрать наименьшее и наибольшее.

И вновь, как и в § 237, следует подчеркнуть, что полученный результат относится лишь к функциям, дифференцируемым в рассматриваемом интервале [а, b] . Если же в этом интервале имеются точки, в которых исследуемая функция не имеет производной, то эти точки следует рассмотреть особо. Абсолютный минимум или абсолютный максимум функции в интервале [а, b]  может достигаться в одной из таких точек (см. рис. 274  в интервале [2, 6]).

Рассмотрим несколько примеров.

Пример 1. Найти наименьшее и наибольшее значения функции f (х)  = x³ — 3x² в интервале  [1, 3].

Имеем:    f (х)  = x³ — 3x²,      f '(х) =3x² — 6х.

Из уравнения  f '(х) = 0, или 3x² — 6х = 0, находим стационарные точки функции  f (х) : x₁ = 0, x₂ = 2. В интервал [1, 3] попадает лишь вторая точка. В ней функция принимает значение f (2) = — 4. В крайних точках интервала [1,3] имеем: f (1) = — 2; f (3) = 0. Из трех значений f (2) = — 4, f (1) = — 2 и f (3) = 0 наименьшим является — 4, а наибольшим 0.

Поэтому минимальное значение функции  f (х)  = x³ — 3x² в интервале [1,3] равно    — 4, максимальное 0. Они достигаются соответственно в точках х = 2 и х = 3.

Пример  2.   Найти наименьшее и наибольшее значения функции  f (х) = ³/₂ х + sin х  в интервале  [а, b].

Имеем:

 f '(х)  = ³/₂ + cos х.

Функция  f '(х) положительна при всех значениях х. Поэтому f (х) монотонно возрастает на всей числовой прямой. В таком случае в левом конце (х = а) интервала [а, b ] эта функция должна принимать наименьшее значение ³/₂ а + sin а, а в правом конце (х = b) — наибольшее значение ³/₂b + sin b.

Упражнения

1916.  Найти  наименьшее  и  наибольшее значения функции у = x³ — 3x в интервалах: а)      [ —0,5; 0,5];     б) [ — 1,5; 2].

1917.  Найти   наименьшее   и   наибольшее   значения   функции у = sin x — √3 cos x  в интервалах: а) [— π; 0];   б)  [ 0;  ^π/₂] .

1918.  Найти наименьшее и наибольшее значения функции у =¹/₂ x³ — ⁵/₂ x² + 6x + 10 в интервалах: а) [0; 1]; б) [0; 2,5]; в) [0; 4].

Найти наименьшие и наибольшие значения данных функций в указанных интервалах (№ 1919—1923):

1919.   у = ¹/₂ x — sin x    в   интервалах:    а) [ 0;  ^π/₂ ] ; б)  [  —  ^π/₄ ; ^π/₄ ] ; в) [ — ^π/₂ ; ^π/₂].

1920.  у = х — cos 2х   в   интервалах:    а) [ — ^π/₂ ; ^π/₂] ;   б)   [— π;  π]; в) [— π; 0].

1921.  у = x⁴ — 8x² — 9 в интервалах: а) [—1; 1 ]; б) [0; 3]; в) [—3; 5].

1922. у =3x⁴ — 4x³ — 72x² + 200 в интервалах: а)[— 1; 1 ]; б) [— 0,5; 3,5]; в)  [— 2; 5].

1923.  у = 1 + 36x + 36x² — 2x³ в интервалах: а) [— 3; — 1 ]; б) [— 2; 2]; в) [—10; 4].

ОТВЕТЫ