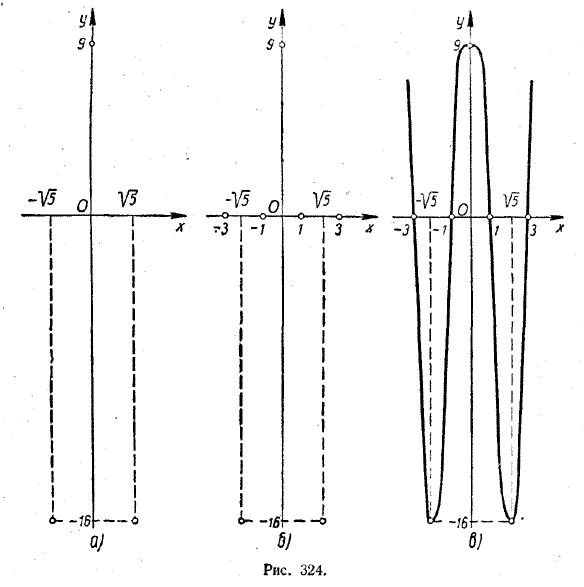
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ K ИССЛЕДОВАНИЮ ФУНКЦИЙ  X

§ 239. Использование производных  для  исследования дифференцируемых функций и построения их графиков

Использование производных значительно облегчает исследование дифференцируемых функций и построение их графиков. С помощью производной можно установить интервалы возрастания и интервалы убывания функций, найти стационарные точки и локальные экстремумы. А это позволяет более точно построить графики исследуемых функций.

В дальнейшем мы будем придерживаться следующего плана* исследования функции  у = f (x):

* Этот план лишь незначительно отличается от плана, описанного в § 210.

1)  область определения функции;

2)  поведение функции вблизи «особых» точек (например,   функции у = ¹/_x вблизи точки х = 0);

3)  четность функции;

4)  периодичность функции;

5)  стационарные точки и локальные экстремумы функции;

6)  интервалы возрастания и интервалы убывания функции;

7)  нули функции, то есть корни уравнения f (x) = 0;

8)  интервалы знакопостоянства функции;

9)  поведение функции при неограниченном возрастании значений аргумента (х—>∞) и   при   неограниченном   убывании   значений   аргумента    (х—> — ∞);

10)  область изменения функции.

Осуществление каждого пункта этого плана полезно сопровождать геометрической интерпретацией, выполняя шаг за шагом построение графика исследуемой функции.

В качестве примера рассмотрим функцию

у = x⁴ — 10x² + 9.   '

1)  Областью определения данной функции является множество всех действительных  чисел.

2)  "Особых" точек (типа точки х = 0 для функции у = ¹/_x) эта функция  не имеет.

3)  Функция четна, поскольку при любом значении х

(—x)⁴ — 10 (—x)² + 9 = x⁴ — 10x² + 9.

Это должно найти свое отражение и в графике функции. Он должен получиться симметричным относительно оси ординат.

4)  Рассматриваемая функция, очевидно, непериодична.

Вообще периодичность той или иной функции часто устанавливается путем простого указания на периодические составляющие этой функции (например, sin х, cos х и т. п.). Данная функция подобных составляющих не имеет. Конечно, это не может служить строгим доказательством непериодичности рассматриваемой функции. Поэтому мы еще вернемся к этому вопросу при рассмотрении пункта 6.

(Впрочем, возможно и такое доказательство непериодичности. Если бы данная функция была периодической с периодом Т > 0, то при любом значении х выполнялось бы равенстно

(х + T)⁴ — 10(х + T)²  + 9 = x⁴ — 10x² + 9.

В частности, при х = 0 мы получили бы

T⁴ — 10T² + 9 = 9,

откуда Т = √10. Таким образом, в качестве периода может выступать лишь число √10. Но, как мы знаем, периодические функции имеют бесконечно много положительных периодов. Получено противоречие. Следовательно, предположение о периодичности данной функции неверно.)

5)  Стационарные точки функции f (x) находятся как корни уравнения f '(x)  = 0. В данном случае f '(x) = 4x³ — 20х;  поэтому нам нужно решить уравнение

4x³ — 20х = 0.

Оно имеет три корня:

x₁ = 0;

x₂ = — √5;

x₃ = √5

Чтобы выяснить, какие из этих трех стационарных точек дают локальные экстремумы и какие именно экстремумы (минимумы или максимумы), рассмотрим поведение производной f '(x)  вблизи стационарных точек. Имеем:

f '(x)  = 4x³ — 20х = 4x (x² — 5).

Если х близко к нулю и х < 0, то оба сомножителя 4x  и x² — 5  отрицательны. B  этом случае  f '(x) > 0.   Если же х близко к нулю и х > 0, то множитель 4х будет положительным,  а множитель x² — 5  — отрицательным.  В этом случае f '(x)  < 0.

При переходе через точку х = 0 производная f '(x)  меняет знак с «+» на «—». Поэтому точка х = 0 является точкой локального максимума функции у = x⁴ — 10x² + 9.

Аналогично устанавливается (сделайте это самостоятельно!), что точки х = — — √5  и х = √5 являются точками локальных минимумов.

Теперь можно найти и сами локальные экстремумы.

При х = 0   у = 9;     при  х = ±√5   у = — 16.

Итак, функция у = x⁴ — 10x² + 9  имеет один локальный максимум, равный 9  (он достигается при х = 0), и два локальных минимума, каждый из которых равен — 16 (они достигаются при х = — √5 и х = √5).

Это   позволяет   нам отметить на координатной плоскости три точки графика нашей функции. Это будут точки с координатами (0,9), (— √5, — 16) и (√5, — 16), причем первая из них служит геометрическим образом локального максимума, а остальные две — геометрическими образами локальных минимумов данной функции (рис. 324, а).

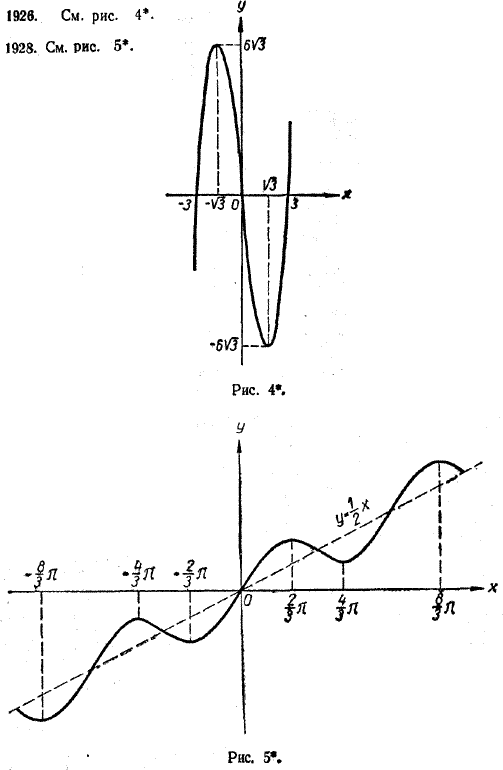
6)  Найдем интервалы возрастания и интервалы убывания,рассматриваемой функции. После исследования стационарных точек легко понять, что при —√5 < х < 0 и х > √5 эта  функция   возрастает,   а   при х < — √5   и  0 < х < √5 убывает (см. рис. 324, а). Но это, конечно, можно доказать и строго, не обращаясь к геометрической интуиции.

Действительно, производная

f '(x)  =  4x (x² — 5)

при —√5 < х < 0 и х > √5  положительна,   а  при  х < — √5   и  0 < х < √5  отрицательна. А это и служит доказательством того, что выше мы  подметили, исходя из геометрических соображений.

Полученный результат, между прочим, доказывает (и притом вполне строго), что функция  у = x⁴ — 10x² + 9  непериодична. Действительно, при х > √5 она монотонно возрастает и, следовательно, значения ее не могут повторяться периодически.

7)   Нули данной функции находятся из уравнения

x⁴ — 10x² + 9 = 0.

Оно имеет четыре корня:

x₁ = — 3,
x₂ = — 1,
x₃= 1
x₄=3.

Симметричность этих корней вполне понятна: ведь рассматриваемая функция (четна.)

Теперь мы можем отметить на плоскости координат еще четыре точки, принадлежащие графику нашей функции. Это точки оси х с абсциссами — 3, — 1, 1 и 3 (см. рис. 324, б).

8)  Очевидно,  что между любыми  двумя соседними  нулями функция f (x) сохраняет   свой знак постоянным*.  

* Это «очевидное» утверждение может быть доказано и совсем строго. Однако доказательство выходит за пределы нашей программы.

Так,  при — 3 < х < — 1  она  принимает либо только положительные, либо только отрицательные значения. Чтобы выяснить, какие именно (по знаку) значения принимает наша функция при — 3 <  х < — 1, достаточно определить ее знак в какой-нибудь одной точке этого интервала. В данном случае удобно выбрать х = — √5 — точку   локального минимума. В ней, как было указано выше, функция принимает значение, равное  — 16. Поэтому  всюду в интервале — 3 < х < — 1  наша функция принимает отрицательные значения.

Аналогично можно установить (сделайте это самостоятельно!), что при — 1 < х < 1 наша функция принимает положительные значения,  а при 1 < х < 3 —  отрицательные значения. Что касается значений функции при | х | > 3, то все они будут положительными.

9)  При   неограниченном   возрастании  х (х—>∞)   и   неограниченном   убывании х (х—> — ∞) значения функции у = x⁴ — 10x² + 9 неограниченно возрастают  (у—>∞).   Этот факт   является   очевидным,   поскольку  с ростом   х величина  x⁴ растет   гораздо быстрее,   чем   10x².   Возможно  и  такое  объяснение:

x⁴ — 10x² + 9 = (x² — 1) (x² — 9).

Когда х—>∞  или х—> — ∞,   то каждый  из сомножителей x² — 1 и x² — 9 неограниченно   растет.   Поэтому   неограниченно    растет   и   их    произведение.

10) Теперь нетрудно определить область изменения исследуемой функции. Минимальное значение, равное — 16, функция принимает в двух точках: х = — √5 и х = √5. Максимального значения она не имеет: при неограниченном росте х (по абсолютной величине) неограниченно растут и значения функции. Поэтому область изменения функции у = x⁴ — 10x² + 9 определяется неравенством у > — 16.

График функции у = x⁴ — 10x² + 9 представлен на рисунке 324, в.

Упражнения

Исследовать данные функции (№ 1924—1930) и построить их графики!

1924.  у = x⁴ — 2x² — 3.                             1928. у = ¹/₂ х + sin x.

1925.  у = ¹/₁₀ (x⁴ — 13x² + 36).                  1929.  у = √3 cos x — 2х.

1926.  у = x³ — 9x.                                       1930*. у = sin² х + 2 cos х + ¹/₄.

1927.  у = x³ — 3x² + 2.

ОТВЕТЫ