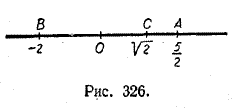КОМПЛЕКСНЫЕ ЧИСЛА     XI

§ 249. Геометрическое изображение комплексных чисел

Как известно (см. ч. I, § 44), действительные числа можно изображать точками числовой прямой. При этом каждому действительному числу соответствует единственная точка числовой прямой. Например, действительному числу ⁵/₂ соответствует точка А (рис. 326), находящаяся справа от начальной точки О на расстоянии в ⁵/₂ единицы   длины;   действительному числу — 2 соответствует точка В, находящаяся слева от точки О на расстоянии в 2 единицы длины;   действительному числу √2 соответствует точка С, находящаяся справа от О на расстоянии в √2 единиц длины.

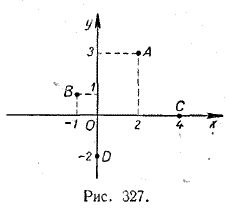
Обратно, каждой точке числовой прямой соответствует вполне определенное действительное число. Например, точкам А и В (рис. 326) соответствуют рациональные  числа ⁵/₂  и —2, а точке С—иррациональное число √2. Таким образом, множество всех действительных чисел находится во взаимно  однозначном  соответствии с множеством всех точек числовой прямой.

Подобно тому как действительные числа можно изображать точками числовой прямой, комплексные числа можно геометрически представлять точками плоскости.

Каждому комплексному числу а + bi поставим в соответствие точку плоскости с координатами (а, b). Например, числу 2 + 3i поставим в соответствие (рис. 327) точку А с координатами (2, 3), числу — 1 + i  — точку В с координатами (— 1, 1), числу 4 + 0i — точку С с координатами (4,0), числу 0 — 2i — точку D с координатами (0, —2) и т. д.

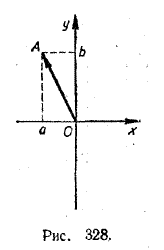
Каждая точка плоскости имеет определенные координаты. Поэтому при выбранном соответствии каждой точке плоскости будет отвечать некоторое комплексное число. Например, точке А с координатами (2, 3) отвечает число 2 + 3i  (рис. 327), точке В с координатами (— 1, 1) — число (— 1 + i), точке С с координатами (4, 0) — число 4 + 0i, а точке D с координатами (0, — 2) — число 0 — 2i. Но не может ли случиться так, что одной и той же точке плоскости, например точке (α, β), будут соответствовать различные комплексные числа, например  а₁ + b₁i  и а₂ + b₂i? Если бы было так, то мы имели бы:

α = а₁ ,  β = b₁;

α = а₂  ,  β = b₂; .

Отсюда а₁ = а₂, b₁ = b₂. Но в таком случае числа а₁ + b₁i  и а₂ + b₂i  были бы равны между собой.

Итак, каждому комплексному числу а + bi соответствует одна, вполне определенная точка плоскости, а именно точка с координатами (а, b). Наоборот, каждой точке плоскости (α, β) соответствует одно, вполне определенное комплексное число, a именно число α + βi. Таким образом, множество всех комплексных чисел находится во взаимно однозначном соответствии с множеством всех точек плоскости.

С каждой точкой плоскости А можно связать вектор OA^> выходящий из начала координат и оканчивающийся в точке А (рис. 328). Поэтому комплексные числа допускают и другую геометрическую интерпретацию.

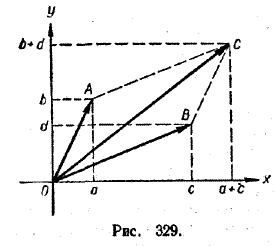
Каждое комплексное   число  а + bi   можно геометрически интерпретировать как вектор OA^> с координатами (а, b). Координаты вектора OA^> при этом будут такими же, как и координаты точки А, а именно (а, b). Очевидно, что такое соответствие между всеми комплексными числами и всеми векторами плоскости, выходящими из начала координат, является также взаимно однозначным.

Используя векторную интерпретацию комплексных чисел, легко истолковать то определение, которое мы приняли для суммы двух комплексных чисел:

 (а + bi) + (с + di) = (а + с) + (b + d)i.

Как   известно,   при   сложении   векторов   их   соответственные координаты складываются.  Поэтому если  вектор  OA^>  (рис. 329) имеет координаты (а,  b), а вектор   OB^> — координаты (с, d), то их сумма — вектор  OC^> — будет иметь координаты (а + с, b + d).

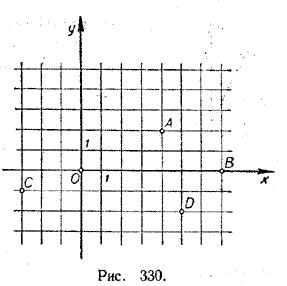
Этот вектор как раз и соответствует комплексному числу (а + с) + (b + d)i , которое является суммой комплексных чисел а + bi и с + di.

К сожалению,  определение  произведения  двух комплексных чисел

(а + bi ) (с + di) = (ac — bd) + (ad + bc) i

не допускает такой простой интерпретации.

Упражнения

1996. Данные  комплексные  числа  изобразить  точками плоскости:

а)   1 + i;           в) —2 + 3i;         д) 5+ 0i;            ж) 0 + 5i

б)  1 — i;           г) —3 — 2i;         е) —6 + 0i;         з) 0 — 4i.

1997.   Какие комплексные числа изображают   на рисунке 330 точки А, В, C,D и О?

1998.  Дать   геометрическую интерпретацию формулам:

а)  (1 +2i) + (l — 2i)=2 + 0i;

б)  (3 — 4i)+(— 1 + 2i) = 2—2i.

1999.  Пусть точка М служит изображением на плоскости комплексного числа а + bi.  Построить на той же плоскости точки, которые изображали бы комплексные числа:

a) а — bi;           д) 0 + bi

б)  — а + bi;      е) — а + 0i;

в)  — а — bi     ж) 0 — bi.

г)  а + 0i;

2000. Пусть точка М служит изображением на плоскости комплексного числа а — bi. Где на той же плоскости расположены точки, изображающие числа:

а)  3а + 0i ;         г) 0 + 2bi

б)  — 5а + 0i;    д) 4а + 3bi .

в) 0 — bi;