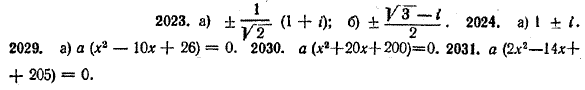КОМПЛЕКСНЫЕ ЧИСЛА     XI

§ 253. Извлечение корней квадратных из отрицательных   чисел.
  Решение   квадратных    уравнений   с   отрицательными    дискриминантами

Как мы знаем,

i² = — 1.

Вместе с тем

(— i)² = (— 1 • i)² = (— 1)² • i² = —1.

Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i и — i . Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi равен — 1. Тогда

(а + bi )² = — 1,

а² + 2аbi— b² = — 1

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях.   Поэтому

Согласно второму уравнению системы (1) хотя бы одно из чисел а и b должно равняться нулю. Если b = 0, то из первого уравнения получается а² = — 1. Число а действительное, и поэтому а² > 0. Неотрицательное число а² не может равняться отрицательному числу — 1. Поэтому равенство b = 0 в данном случае невозможно. Остается признать, что а = 0, но тогда из первого уравнения системы получаем:  — b² = — 1,   b = ± 1.

Следовательно, комплексными числами, квадраты которых равны —1, являются только числа i и —i, Условно это записывается в виде:

√—1 = ± i.

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а. Такими числами являются √a i и —√a i . Условно это записывается так:

√— а = ± √a i.

Под √a здесь подразумевается арифметический, то есть положительный, корень. Например, √4 = 2,  √9 =.3; поэтому

√—4 = + 2i,           √—9= ± 3i   

и  т.   д.

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x² + 2х + 5 = 0; тогда

х_1,2 = — 1 ± √1 —5 = — 1 ± √—4 = — 1 ± 2i.

Итак, данное уравнение имеет два корня: х₁ = — 1 +2i,    х₂ =  — 1 — 2i. Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.

Упражнения

2022.   (У с т н о.)   Решить уравнения:

а) x² = — 16;   б) x² = — 2;    в) 3x² = — 5.

2023.  Найти все комплексные числа, квадраты которых равны:

а) i;        б) ¹/₂ — ^√3/₂ i ;

2024.  Решить квадратные уравнения:

а) x² — 2x + 2 = 0;   б) 4x² + 4x + 5 = 0;   в) x²— 14x + 74 = 0.

Решить системы уравнений (№ 2025, 2026):

2025.

2026.

2027.  Доказать, что корни квадратного уравнения с действительными   коэффициентами    и   отрицательным   дискриминантом являются взаимно сопряженными.

2028.  Доказать,  что теорема Виета верна для любых   квадратных уравнений, а не только для уравнений с неотрицательным дискриминантом.

2029.  Составить   квадратное   уравнение    с   действительными коэффициентами, корнями которого являются:

a) х₁= 5 — i, х₂ = 5 + i;    б) х₁ = 3i,    х₂ = — 3i.

2030.  Составить    квадратное   уравнение   с   действительными коэффициентами, один из корней которого равен (3 — i) (2i — 4).

2031.  Составить   квадратное   уравнение   с   действительными коэффициентами, один из корней которого равен    32 — i
                                                   1— 3i .

ОТВЕТЫ