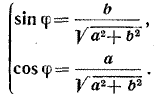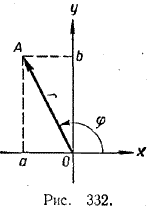
КОМПЛЕКСНЫЕ ЧИСЛА     XI

§ 256. Тригонометрическая  форма  комплексных   чисел

Пусть комплексному числу а + bi соответствует вектор OA^> с координатами (а, b) (см. рис. 332).

Обозначим длину этого вектора через r, а угол, который он образует с осью  х, через φ. По определению синуса и косинуса:

^a/_r = cos φ,      ^b/_r = sin φ.

Поэтому а = r cos φ, b = r sin φ. Но в таком случае комплексное число а + bi можно записать  в  виде:

а + bi = r cos φ + ir sin φ = r (cos φ + i sin φ).

Как известно, квадрат длины любого вектора равен сумме квадратов его координат. Поэтому r² = a² + b², откуда r = √a² + b²

Итак, любое комплексное число   а + bi   можно представить в виде:

а + bi = r (cos φ + i sin φ),            (1)

где   r = √a² + b² ,    а угол φ определяется из условия:

Такая форма  записи  комплексных  чисел   называется   тригонометрической.

Число r  в формуле (1) называется модулем, а угол φ — аргументом, комплексного числа   а + bi  .

Если комплексное число  а + bi  не равно нулю, то модуль его положителен; если же     а + bi  = 0, то а = b = 0 и тогда r = 0.

Модуль любого комплексного числа определен однозначно.

Если комплексное число   а + bi   не равно нулю, то аргумент его определяется формулами (2) однозначно с точностью до угла, кратного 2π. Если же   а + bi  = 0, то а = b = 0. В этом случае r = 0. Из формулы (1) легко понять, что в качестве аргумента φ в данном случае можно выбрать любой угол:   ведь при  любом   φ

0 • (cos φ + i sin φ) = 0.

Поэтому аргумент нуля не определен.

Модуль комплексного числа r иногда обозначают | z |, а аргумент arg z. Рассмотрим несколько примеров на представление комплексных  чисел   в тригонометрической форме.

Пример . 1. Записать в тригонометрической форме комплексное  число   1 + i.

Найдем модуль r и аргумент φ этого числа.

r = √1² + 1²  = √2.

Следовательно, sin φ = ¹/_√2 , cos φ = ¹/_√2 , откуда φ = ^π/₄ + 2nπ.

Таким   образом,

1 + i = √2 [cos (^π/₄ + 2nπ) + i sin (^π/₄ + 2nπ)],

где п — любое целое число. Обычно из бесконечного множества значений аргумента комплексного числа выбирают то, которое заключено между 0 и 2π. В данном случае таким значением является ^π/₄.  Поэтому

1 + i = √2 (cos ^π/₄  + i sin ^π/₄ )

Пример   2. Записать в тригонометрической форме комплексное число √3 — i. Имеем:

r = √3+1 = 2,      cos φ = ^√3/₂ ,   sin φ = — ¹/₂

Поэтому с точностью до угла,  кратного 2π,   φ = ¹¹/₆ π; следовательно,

√3 — i = 2( cos ¹¹/₆ π + i sin ¹¹/₆ π).

Пример 3  Записать в тригонометрической форме комплексное число i .

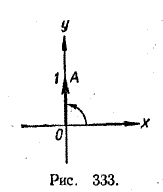
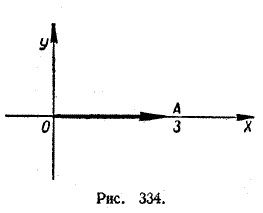
Комплексному числу i соответствует вектор OA^>, оканчивающийся в точке А оси у с ординатой 1 (рис. 333). Длина такого вектора равна 1,   а угол, который он образует с   осью абсцисс, равен ^π/₂.    Поэтому

i = cos ^π/₂ + i sin ^π/₂.

Пример 4. Записать в тригонометрической форме комплексное  число  3.

Комплексному числу 3 соответствует вектор OA^>, оканчивающийся в точке оси  х  абсциссой   3   (рис. 334).   

Длина такого вектора равна 3, а угол, который он образует с осью абсцисс, равен 0. Поэтому

3 = 3 (cos 0 + i sin 0),

Пример 5. Записать в тригонометрической форме комплексное число —5.

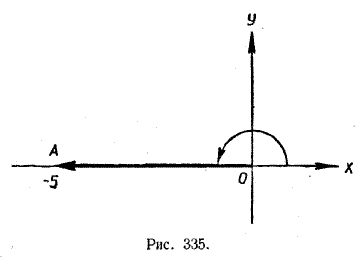
Комплексному, числу —5 соответствует вектор  OA^>, оканчивающийся в точке оси х с   абсциссой —5 (рис. 335). Длина такого вектора равна 5, а угол,   который он образует с осью абсцисс, равен π. Поэтому

—5 = 5(cos π + i sin π).

Упражнения

2047.  Данные  комплексные  числа  записать   в  тригонометрической форме, определив их модули и аргументы:

1)  2 + 2√3i ,        4) 12i  — 5;         7).3i ;

2)  √3 + i ;             5) 25;               8) —2i ;

3)  6 — 6i ;               6) — 4;               9) 3i  — 4.

2048.  Указать на плоскости множества точек,   изображающих комплексные числа, модули г и аргументы ф которых  удовлетворяют условиям:

1) r = 1,   φ = ^π/₄;       4) r < 3;              7) 0 < φ < ^π/₆;

2) r =2;                       5) 2 < r <3;          8)  0 < φ < я;

3)  r < 3;                     6) φ = ^π/₃;            9) 1 < r < 2,

                                                              10) 0 < φ < ^π/₂ .

2049.  Могут  ли   модулем   комплексного   числа   одновременно быть числа r и  — r?

2050.  Могут ли аргументом комплексного числа одновременно быть углы φ и — φ?

Данные комплексные числа представить в тригонометрической форме,  определив их модули и  аргументы:

2051*. 1 + cos α + i sin α.              2054*. 2(cos 20° — i sin 20°).

2052*. sin φ + i cos φ.                   2055*. 3(— cos 15° — i sin 15°).

2053*. —5 (cos 40° — i sin 40°).

ОТВЕТЫ