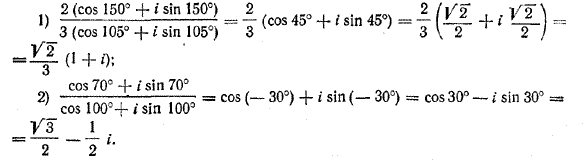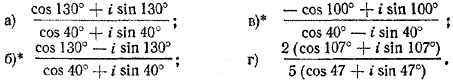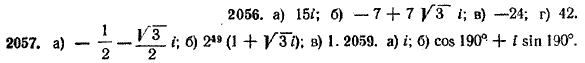КОМПЛЕКСНЫЕ ЧИСЛА     XI

§ 257. Умножение и деление комплексных   чисел,   заданных   в тригонометрической форме

Умножение и деление комплексных чисел удобнее выполнять, если эти числа заданы в тригонометрической форме. Имеют место следующие теоремы.

Теорема 1. Модуль произведения двух комплексных чисел равен произведению их модулей, а аргумент — сумме их аргументов.

Доказательство.    Пусть

z₁ = r₁ (cos φ₁ + i sin φ₁),        z₂ = r₂ (cos φ₂ + i sin φ₂).

Тогда

z₁ • z₂ = r₁ • r₂ (cos φ₁ + i sin φ₁) (cos φ₂ + i sin φ₂) =

= r₁ • r₂ (cos φ₁ • cos φ₂ +   cos φ₁ • sin φ₂+ i sin φ₁ •  cos φ₂ — sin φ₁• sin φ₂) =

=  r₁ • r₂ [(cos φ₁ • cos φ₂—sin φ₁ • sin φ₂) + i (sin φ₁ • cos φ₂ + cos φ₁ • sin φ₂)];

но

cos φ₁ • cos φ₂—sin φ₁ • sin φ₂ = cos (φ₁ + φ₂);

sin φ₁ • cos φ₂ + cos φ₁ • sin φ₂ = sin (φ₁ + φ₂).

Поэтому

z₁z₂ = r₁r₂ [cos (φ₁ + φ₂) + i sin (φ₁ + φ₂)].

А это и означает, что модуль произведения z₁ • z₂  равен произведению модулей чисел z₁ и z₂, а аргумент произведения — сумме аргументов чисел z₁ и z₂. Теорема 1 доказана.

Примеры.

2 (cos 130° + i sin 130°) • 3 (cos 230° + i sin 230°) = 6 (cos 360° + i sin 360°) = 6.

5 (cos 47° + i sin 47°) • 4 (cos 13° + i sin 13°) = 20 (cos 60° + i sin 60°) =

= 20 ( ¹/₂ + i ^√3/₂ ) = 10+10√3 i.

Отметим, что доказанная теорема справедлива для любого числа сомножителей, то есть при любом п:

r₁ (cos φ₁ + i sin φ₁)  •  r₂ (cos φ₂ + i sin φ₂)  ...  r_n (cos φ_n + i sin φ_n)  =

= r₁r₂ . . . r_n  [cos (φ₁ + φ₂ + . . . + φ_n) + i sin (φ₁ + φ₂ + . . . + φ_n)].

В частном случае, когда все сомножители равны между собой, получаем:

[r (cos φ + i sin φ) ]ⁿ = rⁿ [cos пφ + i sin пφ ].

Эта формула носит   название  формулы   Муавра*.   

* М у а в р  (1667—1754) — английский математик.

При r =1   она  принимает вид:

(cos φ + i sin φ)ⁿ = cos пφ + i sin пφ.

Теорема 2. Модуль частного двух комплексных чисел равен частному модулей делимого и делителя; аргумент частного двух не равных нулю комплексных чисел равен разности аргументов делимого и делителя.

Доказательство.

Обозначим частное от деления комплексного числа z₁ = r₁ (cos φ₁ + i sin φ₁)  на комплексное число z₂ = r₂ (cos φ₂ + i sin φ₂) =/= 0  через z = r (cos φ + i sin φ). Тогда z = z₁/z₂ , или z • z₂ = z₁. Поэтому

r (cos φ + i sin φ) • r₂ (cos φ₂ + i sin φ₂) = r₁ (cos φ₁ + i sin φ₁) .

Производя умножение в левой части этого равенства, получаем:

rr₂ [cos (φ + φ₂) + i sin (φ + φ₂)] = r₁ (cos φ₁ + i sin φ₁) .

Модули двух равных комплексных чисел, отличных от нуля, равны, а аргументы могут отличаться лишь на угол, кратный 2π. Поэтому из последнего равенства вытекает, что

rr₂ = r₁ ;    φ + φ₂ — φ₁ = 2пπ

где п — некоторое целое число.

Следовательно,

r = r₁/r₂,  φ = φ₁  — φ₂ + 2пπ.

Аргумент любого комплексного числа, отличного от нуля, определен лишь с точностью до угла, кратного 2π. Поэтому можно считать, что аргумент φ комплексного числа z  равен

φ₁  — φ₂

Теорема   доказана.

Примеры.

Упражнения

2056.  Выполнить указанные действия:

а) 5 (cos 40° +  i sin 40°) • 3 (cos 50° + i sin 50°);

б)  2 (cos 20° + i sin 20°) • 7 (cos 100° + i sin 100°);

в)  4 ( cos ^π/₈ + i sin ^π/₈) • 6 (cos ⁷/₈ π + i sin ⁷/₈ π );

г) 7 ( cos ⁸/₁₅ π + i sin ⁸/₁₅ π) • 3  (cos ²/₃ π + i sin ²/₃ π) •2  (cos ⁴/₅ π + i sin ⁴/₅ π )

2057.  Вычислить:

a) ( ^√3/₂— ¹/₂ i ) ¹⁰⁰;     б)  (√3 + i )⁵⁰ ;      в) (¹/_√2 + i ¹/_√2)⁸'

2058.  Как изменяется модуль и аргумент комплексного числа в результате умножения этого числа на:

а)       i;        в)     2i ;      д)     4;

б)  —  i ;         г) — 3i;        e) —5?

2059.  Выполнить деление:

2060.   Как изменятся модуль  и аргумент комплексного числа в результате деления этого числа на: a) i; б) — i?

ОТВЕТЫ