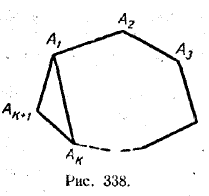
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ    XII

§ 263. Другой вариант метода математической индукции

Некоторые утверждения справедливы не для всех натуральных п, а лишь для натуральных п, начиная с некоторого числа р. Такие утверждения иногда удается доказать методом, несколько отличным от того, который описан в § 262, но вполне аналогичным ему. Состоит он в следующем.

Утверждение верно при всех натуральных значениях п > р, если:

1)  оно верно при п = р (а не при п = 1, как было в § 262);

2)   из справедливости этого утверждения при п = k, где k > p (а не k > 1, как в § 262), вытекает, что оно верно и при  n = k + 1.

Поясним это на следующем примере.

Доказать, что сумма  S_n  внутренних углов любого выпуклого многоугольника равна     (п—2)π, где п — число   сторон   этого многоугольника*:

S_n  = (п — 2)π                (1)

* Это утверждение верно и для невыпуклых многоугольников, если, правда, стороны их пересекаются только в вершинах. Мы же для простоты ограничиваемся лишь выпуклыми многоугольниками.

Это утверждение имеет смысл не для всех натуральных п, а лишь для п > 3. Поэтому метод, описанный в § 262, здесь использовать нельзя. Однако можно использовать другой вариант индукции, описанный выше.

1)   При п = 3 наше утверждение принимает вид: S₃ = π. Но сумма  внутренних   углов любого  треугольника действительно равна п. Поэтому при п = 3 формула (1) верна.

2)  Пусть эта формула верна при п — k, то есть S_k = (k — 2)π, где k >  3. Докажем,  что   в  таком  случае  имеет  место  и формула S_k+1 = (k — 1)π.

Пусть A₁A₂ ... A_kA_k+1—произвольный выпуклый (k + 1) -угольник (рис. 338).

Соединив точки A₁ и A_k, мы получим выпуклый k-угольник A₁A₂ ... A_{k— 1}A_k. Очевидно, что сумма углов (k + 1) -угольника A₁A₂ ... A_kA_k+1 равна сумме углов k-угольника A₁A₂ ... A_k плюс сумма углов треугольника A₁A_kA_k+1. Но сумма углов k-угольника A₁A₂ ... A_k  по предположению равна (k — 2)π, а сумма углов треугольника A₁A_kA_k+1 равна π. Поэтому

S_k+1= S_k + π = (k — 2)π + π  = (k — 1)π.

Итак, оба условия принципа математической индукции выполняются, и потому формула (1) верна при любом натуральном п > 3.

Упражнения

2106.   На сколько треугольников может быть разбит выпуклый n - угольник своими непересекающимися диагоналями?

2107.  Доказать,   что   при   п > 3

2ⁿ >2п + 1.

2108.  При каких натуральных значениях п справедливо неравенство

2ⁿ >  n²  ?