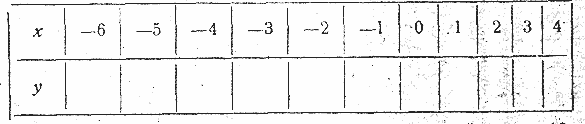
ГЛАВА  XIV

ФУНКЦИИ И ИХ ГРАФИКИ.

§ 63. Функция    у = ax²  + bx + c     и её график.

1804. С высоты 5 м выпущена из лука вертикально вверх стрела с начальной скоростью 50 м в сек.

1) Составить таблицу изменения высоты полёта стрелы в зависимости от изменения времени от начала её движения    до   падения     на    землю,    пользуясь   формулой

, где H— высота стрелы в метрах,  t — время движения в секундах, g ≈ 10 м/сек² — ускорение силы тяжести.

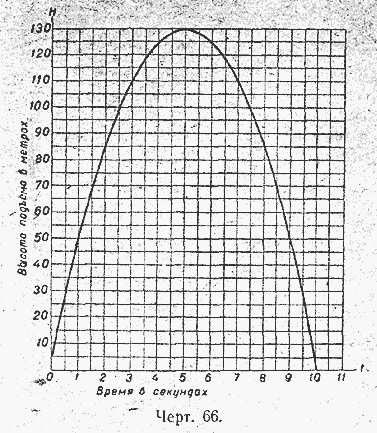
2) Построить график изменения высоты стрелы, откладывая по горизонтальной оси значения t, а по вертикальной оси значения Н . (черт. 66).

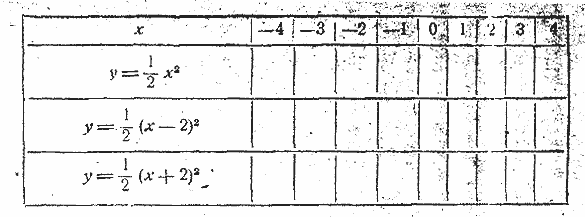
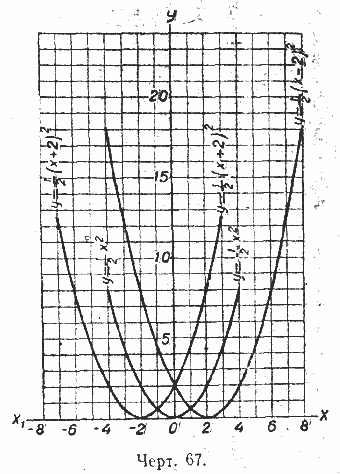
3) Найти по графику и проверить вычислением:

а) Через  сколько  секунд от начала движения стрела упадёт на землю?

б) Через сколько секунд стрела достигнет наибольшей высоты?

в) На сколько метров  от земли  поднялась стрела в  наивысшей точке подъёма?

1805.  1) При  одних   и тех  же осях и в одном и том же масштабе построить графики функций (черт. 67):

составив следующую таблицу, частных значений функций:

2)  Найти  на графиках  (черт.  67) точку  каждой  из кривых, имеющую ординату, равную 8, и убедиться, что соответствующая  абсцисса    точки    графика  у =  ¹/₂ (х — 2)² будет на 2 больше, а абсцисса точки графика у =  ¹/₂ (х + 2)²  на 2 меньше абсциссы точки графика    у =  ¹/₂ х ².

Проверить это свойство данных кривых графически и вычислением для любых точек с равными ординатами.

3)   Выяснить  различие в расположении графиков данных  функций относительно   осей    координат.

4)  Найти   координаты    вершины    каждой, параболы   и   выяснить, каким перемещением параболы  у =  ¹/₂ х ² получена парабола у =  ¹/₂ (х — 2)²  и парабола у =  ¹/₂ (х + 2)².

5)  Определить  по  графикам,  при каких значениях х  каждая  из функций убывает; возрастает; принимает наименьшее значение.

1806.  Даны функции:

а) у = — ¹/₄ х ²     б) у = — ¹/₄ (х — 2)²       в) у = — ¹/₄ (х + 2)².

Построить  графики  этих функций и исследовать их, используя указания и вопросы предыдущей задачи.

1807.  Дана функция:

у =  (х — 4)²

Не вычерчивая графика этой функции, описать:

1)  вид  и  положение кривой относительно осей координат;

2)  будет ли функция иметь наибольшее или наименьшее значение, какое именно и при каком значении х;

3)  при каких значениях х функция у убывает; возрастает; обращается в нуль;

4)  в  какой  точке  пересечёт данная   кривая ось OY;

5)  ответить на вопросы 1 — 4 при следующих данных:

а) у = —  (х + 5)² ;

б) у =  2 (х — 1)² ;

в)  у = — 3 (х — 6)²

1808. Дана функция:

у = х²  — 4х + 4.

1)  Представить правую часть уравнения в виде квадрата двучлена.

2)  Доказать, что  при  любых значениях х функция у не имеет отрицательных значений.

3)  Выяснить, при каких значениях х функция у убывает; возрастает; имеет наименьшее или наибольшее значение; обращается в нуль.

4)  Построить график данной функции, определив предварительно  вычислением   координаты   нескольких   точек (например, точку наименьшего или наибольшего значения функции, точки пересечения   графика с осями координат и т. д.).

Пользуясь   указаниями   предыдущей   задачи, исследовать квадратные трёхчлены и построить их графики:

1809.   1) у = х²  + 2х + 1;     2) у = х²  —  х + ¹/₄.

1810.   1) у = —х²  + 6х — 9;     2) у = —х²  — 8х — 16.

1811.    1) При   каком  условии   квадратный   трёхчлен у = x²  + px + q представляет полный, квадрат двучлена?

2)  Как расположена в этом случае парабола  относительно осей координат?

3)  При  каком   условии   квадратный трёхчлен   имеет наибольшее или наименьшее значение?

4)  Как вычислить  координаты вершины параболы по коэффициентам трёхчлена?

1812.  Дан квадратный трёхчлен:

у = 2 х²  — 4х + 2.

1)  Разложить правую  чисть уравнения на множители и  выяснить,   при  каких значениях  х функция   у  имеет наименьшее значение; убывает; возрастает.

2)  На одном и том же чертеже построить  графики функций:

у = 2 х²        и       у = 2 х²  — 4х + 2..

3)  Выяснить  по графикам сходство и различие полученных кривых.

4)  Найти   координаты   вершин   парабол   и   сравнить расположение кривых относительно осей координат.

1813.   Пользуясь  указаниями предыдущей задачи, исследовать квадратные трёхчлены:

1)  у = —3х²  — 6х — 3;

2)  у = —¹/₂ х²  — 2х —2.

1814.   1) При   каком   условии   квадратный   трёхчлен у = ax²  + bx + c представляет полный квадрат двучлена?

2)  Как   вычисляются   при   этом   условии  координаты вершины параболы по коэффициентам трёхчлена?

1815.  Дана парабола: у = х².

Написать  уравнение каждой из парабол, полученных путём следующих перемещений данной параболы:

1)  парабола перенесена на 5 единиц вверх;

2)  парабола перенесена на 4 единицы вниз;

3)  парабола  перенесена вправо на 3 единицы;

4)  парабола перенесёна на б единиц влево;

5)  направление ветвей параболы изменено на противоположное, и парабола перенесена на 7 единиц влево;

6)  дать для   каждого случая график, начерченный от руки (без точного построения).

1816. Зависимость между х и у выражается уравнением  

 y = x²  + px + q 

Найти значение коэффициентов р и  q, если известно, что:

1)  функция  у обращается в нуль лишь при х = — 2;

2)  функция у имеет наименьшее значение, равное 3, при х = 0;

3)  график,функции касается оси ОХ в точке (—6; 0);

4)  по   составленным уравнениям   начертить   график каждой из функций на одном и том же чертеже.

1817. 1) На одном  и том же чертеже построить графики функций:

у =  (х — 2)²   и     у =  (х — 2)² — 9,

заполнив предварительно следующую таблицу:

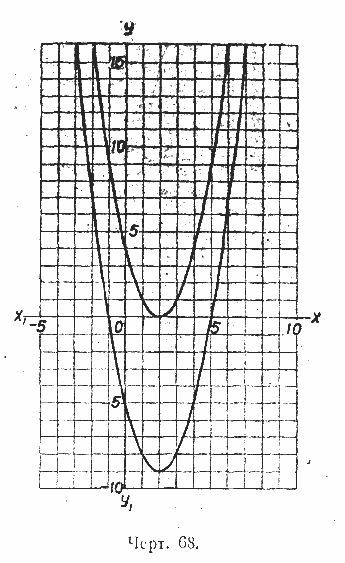
2)   Сравнить     графики     функций    у =  (х — 2)²   и     у =  (х — 2)² — 9 и положение  парабол относительно осей координат (черт. 68).

3)  Найти по графику значения х, при которых функция  у =  (х — 2)² — 9 обращается в нуль, и проверить результат путём решения соответствующего уравнения.

4)    Выяснить,     при    каких    значениях   х   функция  у =  (х — 2)² — 9 убывает; имеет наименьшее значение; возрастает.

5)  Проверить по графику и вычислением, что функция  у =  (х — 2)² — 9 имеет:

а) положительные значения при х < —1 и при   х >5;

6)  отрицательные значения при   —1<  х  <   5.

6) Найти координаты вершины параболы у =  (х — 2)² — 9.

1818. 1)   Квадратный  трёхчлен  у = х ² — 6х + 4   привести к виду у =  (х — 3)²  — 5.

2) Вычислить значения х, при которых функция у обращается в нуль.

3) По уравнению у =  (х — 3)²  — 5   найти координаты  вершины параболы.

4)  Определить    значения   х,  при  которых функция:        

а)   у > 0;   б)  у  <  0;   в)  убывает;   г) возрастает;   д)  имеет наименьшее значение.

5)   На основании полученных результатов начертить схематический   (от  руки) график функции  у =  (х — 3)²  — 5.

1819.   1) В квадратном трёхчлене у = х ² — 4х + 5  выделить полный квадрат.

2) Найти   наименьшее   значение  функции и   координаты вершины параболы.

3) Доказать, что функция у =  (х + 2)²  + 1 не имеет корней (действительных).

4)  Выяснить путём исследования выражения (х + 2)²  + 1 что при любых значениях х функция у > 0.

5)   Построить  график  функции, вычислив координаты следующих точек:

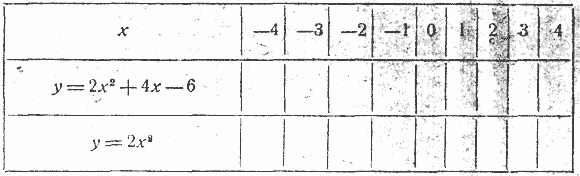
6)  Исследовать, квадратный трёхчлен у = — х²  + 6х — 12, используя указания 1) — 5)

1820. 1) Написать уравнение каждой из парабол, полученных путём следующих перемещений данной параболы:

а) парабола у =  х² перенесена на 4 единицы вправо и на  3 единицы вниз;  

б) парабола у = — х² перенесена на 5 единиц, влево и на 2 единицы вверх;

в) парабола у =  х² перенесена на 6 единиц влево и на 5 единиц вниз.

2) В каждом случае:

а)  построить график функции;

б)  найти  те  значения х, при которых функция у обращается в нуль;

в)  найти   те  значения  х,   при   которых  функция у имеет наибольшее или наименьшее значение.

1821.  Квадратный трёхчлен имеет вид:

у =  x²  + px + q 

1)  При каком условии трёхчлен имеет: а) два различных корня? б) два одинаковых корня? в) не имеет корней (действительных)?

2)  При каком значении х трёхчлен имеет наименьшее значение?

3)  Как  находятся  координаты  вершины параболы по коэффициентам р и q?

1822.  Квадратный трёхчлен имеет вид:

у =  x²  + px + q 

1)  Найти значения р и q:

а)  если функция  у обращается  в нуль при x₁ = 2 и при x₂ = — 3;

б)  если  наименьшее значение функции равно (—2) и функция имеет это значение при   x= 5;

в)  если  график функции  пересекает ось х в точках (—4; 0) и (—1; 0).

2)  В каждом случае начертить (на одном чертеже) график функции и определить, при каких значениях х:

а) функция у > 0; б) у = 0; в) у <0.

1823. 1) Квадратный  трёхчлен у = 2х²  + 4х  — 6 привести к виду:

у = 2(х + 1)²  — 8.

2)  Вычислить значения х, при которых функция у обращается в нуль.

3) Выяснить путём исследования выражения  у = 2(х + 1)²  — 8, что функция:

а) принимает при х = —1 наименьшее значение, равное (—8);

б)  при х <  —3 и при х > 1 функция у > 0;  ;

в)  при  — 3< х <4 функция  у  < 0.

4) На основании полученных результатов, построить график изменения функции у в зависимости от изменения х найдя частные значения х и у по таблице:

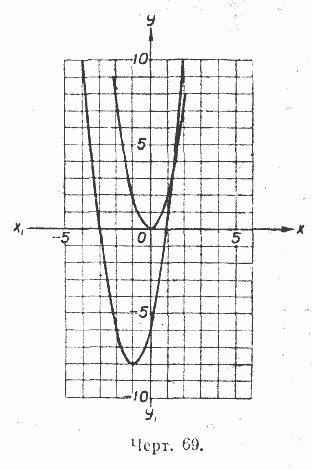
5)  На-том же чертеже и в том же масштабе построить график функции  у = 2х² (черт. 69)

6)  Сопоставить   полученные  графики  и их уравнения и выяснить положение парабол   относительно   осей координат.

7)     Найти     координаты     вершины     параболы у = 2х²  + 4х  — 6   и   выразить их через коэффициенты трёхчлена.'

1824.  1) Используя указания   предыдущей   задачи    исследовать   трёхчлен

у = —  2х²  — 4х +  6

2)  Выяснить,   что данный трёхчлен:'

а)  обращается   в   нуль при x₁ = — 3 и x₂ = 1;

б)    имеет    наибольшее значение у = 8 при  х =—1;

в)  у  <  0 при х < — 3 и   х  >  1;

г) у  >  0 при — 3<  х  < 1

3)   Построить     график трёхчлена.

1825.       1)     Доказать,      что     квадратный    трёхчлен у = 2х²  — 4х +  6 не имеет корней (действительных).

2)  Привести данный трёхчлен к виду    у = 2(х — 1)²+ 4   и доказать, что при любых (действительных) значениях х функция у > 0.

3)  Доказать, что при х = 1 трёхчлен имеет наименьшее значение, и вычислить это значение.

4) Выяснить, что при изменении х от—∞ до 1 функция у убывает от + ∞ до 4; а при изменении х от 1 до + ∞ функция у возрастает от 4 до + ∞. Начертить схематически график данной функции.

1826.   Дан  квадратный  трёхчлен  у = —2х²  + 4х —  6.

1)  Доказать, что этот трёхчлен не имеет корней (действительных).

2)  Доказать, что при любых значениях х функция у  < 0.

3)  Найти, при каком значении х трёхчлен имеет наибольшее значение и какое именно.

4)  Определить,   как  изменяется функция у при изменении х от — ∞  до + ∞ .

5)  Построить график этой функции.

1827. Проверить,   что  координаты вершины параболы у = —2х²  + 4х —  6 определяются по формулам:

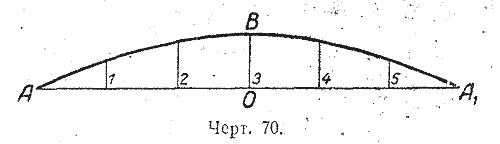
где а, b и с —  коэффициенты трёхчлена.

1828*. 1) Периметр прямоугольника равен 16 см. Таких прямоугольников может быть бесконечное множество; найти тот из них, площадь которого наибольшая.

2)  Из всех прямоугольных  треугольников,   сумма катетов которых равна 12 см, найти треугольник, имеющий наибольшую площадь.

1829*. Для каждого из следующих квадратных трёхчленов определить:

а)   при  каких   значениях   аргумента   трёхчлен   обращается в нуль; принимает положительные или отрицательные значения;

б)  при    каком   значении   аргумента   трёхчлен  имеет наименьшее   или  наибольшее  значение  и   какое именно;

в)  построить график трёхчлена:

1) f (х) = х²  — 4х +  3 ;      2) f (p)= —3p²  + 4p —  5 ;

3)  f (t) = — t²  + 7t —  12 ;     4) f (n) = —4n²  + 12n   — 9;

5) f (r) = 3r²  —  5r  + 2.

1830. Решить графически следующие уравнения:

1) х²  — 7х + 12 = 0;     2) х²  + х  —6 = 0;

3) х²  + 3х +  2 = 0;       4) х²  — 3х  — 4 = 0.

1831*. Арка моста имеет форму дуги параболы, вершина которой находится в середине этой дуги (черт. 70).

Арка имеет 5 вертикальных  стоек,  поставленных через равноотстоящие точки хорды, стягивающей арку. Найти длины этих стоек, если хорда равна 2d,  а высота арки равна h.

Решить задачу при 2d = 108м;   h = 13,5 м.

1832*. Решить неравенства при помощи построения графика:

1) х²  — 2х  — 15 < 0;     2) х²  — 7х + 12 > 0;

3) х²  + 3х  — 40 > 0;     4) х²  — 4х + 3 < 0.

ОТВЕТЫ