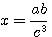| АЛГЕБРА В НАЧАЛО | ||||||||||||||||||||||||||||||||||||
|
ЛОГАРИФМЫ. |
||||||||||||||||||||||||||||||||||||
|
Глава первая. |
||||||||||||||||||||||||||||||||||||
|
Общие свойства логарифмов.
|
||||||||||||||||||||||||||||||||||||
|
1.Два действия, обратные возведению в степень. |
||||||||||||||||||||||||||||||||||||
|
Возьмем такие равенства: |
||||||||||||||||||||||||||||||||||||
|
23 = 2 . 2 . 2 = 8 |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Эти три примера выражают собой различные случаи действия, называемого возведением в степень. Таких действий можно указать следующие два: 1) Пусть требуется узнать, какое число надо возвести в степень с показателем 3, чтобы получить число 12. Обозначив искомое число буквой х, мы можем написать уравнение: | ||||||||||||||||||||||||||||||||||||
|
х3=12 |
||||||||||||||||||||||||||||||||||||
| Действие, посредством которого находится основание х по данной степени и данному показателю ее, называется извлечением корня; оно обозначается, как мы знаем, так: | ||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
2) Положим, надо узнать, какой показатель должен быть у степени, в которую надо возвести основание 4, чтобы получить 16.Обозначив искомый показатель буквой х, можем написать уравнение: |
||||||||||||||||||||||||||||||||||||
|
4х = 16 |
||||||||||||||||||||||||||||||||||||
|
Действие, посредством которого находится показатель степени по данной степени и данному основанию, называется нахождением логарифма данного числа (16) по данному основанию (4). В нашем примере х = 2, так как 42 = 16. |
||||||||||||||||||||||||||||||||||||
|
Итак, возведение в степень имеет два обратных действия. Поставим вопрос, различны ли эти действия? Однако действия эти рассматриваются не как различные, а как одно и то же действие, называемое делением. Причина слияния этих двух обратных действий в одно заключается в переместительном свойстве умножения, по которохму произведение не меняется от перемены мест 1-го и 2-го сомножителя . В таком же положении находится и сложение (2 слагаемых); этому действию также можно указать два обратных действия — нахождение неизвестного числа (1-го слагаемого), к которому надо прибавить данное число (2-е слагаемое), чтобы получить данную сумму; другое — нахождение неизвестного числа (2-го слагаемого), которое надо прибавить к данному числу (к 1-му слагаемому), чтобы получить данную сумму. Однако эти два действия рассматриваются как одно, называемое вычитанием, вследствие того, что сложение обладает переместительным свойством, по которому сумма не зависит от порядка слагаемых. Если бы это свойство принадлежало также и возведению в степень, то тогда и два указанных выше обратных действия составляли бы в сущности одно. Но возведение в степень не обладает свойством переместительности; напр., 23 не равно 32, 102 не равно 210 и т. д. Вследствие этого нахождение основания по данным показателю и степени (извлечение корня) существенно отличается от нахождения показателя по данным основанию и степени (нахождение логарифма). Заметим, что последнее действие в элементарной алгебре подробно не рассматривается; указываются главным образом его практические применения. |
||||||||||||||||||||||||||||||||||||
|
2. Определение логарифма.
|
||||||||||||||||||||||||||||||||||||
|
Если, напр., основание будет 4, то |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
Если возьмем за основание 10, то |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
Вместо того, чтобы писать: „логарифм числа 16 по основанию 4" пишут сокращенно так: | ||||||||||||||||||||||||||||||||||||
|
log4 16, |
||||||||||||||||||||||||||||||||||||
|
помещая внизу знака log то число, которое служит основанием. или |
||||||||||||||||||||||||||||||||||||
|
Прежде чем говорить о применениях логарифмов, мы предварительно рассмотрим свойства так называемой логарифмической функции. |
||||||||||||||||||||||||||||||||||||
|
3.Логарифмическая функция и ее график. Если в равенстве у = аx мы рассматриваем показатель х как независимое переменное , то тогда у будет функция от х, которую мы назвали раньше показательной. Но если в этом равенстве за независимое переменное мы будем считать у, то тогда х будет некоторая функция от у, а именно х есть логарифм числа у по основанию а, что можно выразить так: |
||||||||||||||||||||||||||||||||||||
|
x = loga y |
||||||||||||||||||||||||||||||||||||
|
Обозначая по принятому независимое переменное буквой х, а функцию от этого переменного буквой у (т. е. заменяя х на у и наоборот), мы ту же самую функцию можем записать так: |
||||||||||||||||||||||||||||||||||||
|
y = loga x |
||||||||||||||||||||||||||||||||||||
|
Такая функция называется логарифмической. Логарифмическая функция обратна показательной.(Алгебраическое выражение, полученное для х после решения уравнения, определяющего у как функцию от х, называется функцией, обратной той, которая определяет у) |
||||||||||||||||||||||||||||||||||||
|
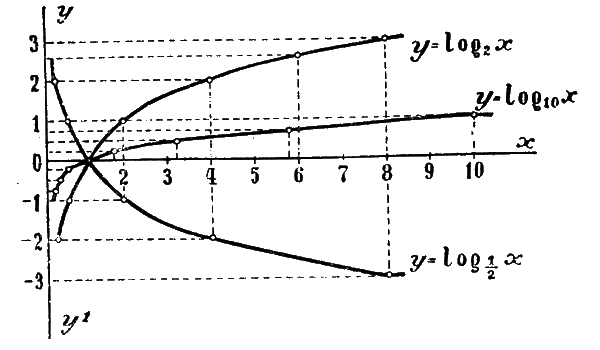
Построим графики следующих трех логарифмических функций: |
||||||||||||||||||||||||||||||||||||
|
1) y = log2х; 2) y = log1/2x; 3) y = log10x. |
||||||||||||||||||||||||||||||||||||
|
Для этого составим таблицы значений этих функций. Всего проще их можно сделать из таблиц соответственных показательных функций |
||||||||||||||||||||||||||||||||||||
|
1)у = 2х; 2) |
||||||||||||||||||||||||||||||||||||
|
поменяв в этих таблицах значения абсциссы х на значения ординаты у и наoборот. Сделав это, мы получим такие 3 таблицы: |
||||||||||||||||||||||||||||||||||||
|
1) y = log2х |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
2) y = log1/2x |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
3) y = log10x |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
Нанеся все эти значения на чертеж и обведя все точки непрерывными кривыми, получим три графика взятых функций. Согласно свойству обратных функций , кривые эти — те же самые, которыми выражаются функции у = 2х; |
||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||
|
Имея график логарифмической функции, мы можем при помощи его найти логарифм (приближенный) числа, помещающегося между взятыми для чертежа значениями x. Возьмем, напр., график функции у = log2x и найдем при его помощи log2 6. |
||||||||||||||||||||||||||||||||||||
|
4. Свойства логарифмической функции. 1) Так как графики всецело расположены направо от оси у -ов, то отрицательные числа не имеют логарифмов (вспомним, что при всяком значении х функция ах положительна). Следовательно, Областью определения логарифмической функции служит множество всех положительных чисел. 2) Всякой положительной абсциссе соответствует своя определенная ордината; значит, всякое положительное число имеет логарифм. Областью изменения логарифмической функции служит множество всех чисел. 3) Все кривые пересекаются с осью х-ов в одной и той же точке, отстоящей от начала координат на + l. Это значит, что при всяком основании логарифм единицы есть нуль (а0 =1). 4) Когда a >1, то части кривых, соответствующие абсциссам, меньшим 1, лежат в угле x0y', а части кривых, соответствующие абсциссам, большим. 1, расположены в угле х0у. Это значит, что при основании, большем 1, логарифмы чисел, меньших 1, отрицательны, а логарифмы чисел, больших 1, положительны. Это вполне соответствует тому свойству показательной функции, что при положительном
значении х функция ах больше 1, а при отрицательном - меньше 1 (если а > 1). 5) Логарифм самого основания равен 1; так, на графике у = log2 x видно, что абсциссе 2 соответствует ордината 1; на других графиках видно то же самое. 6) При основании, большем 1, ветви кривых, расположенные ниже оси x-ов, при уменьшении абсциссы от 1 до 0, приближаются к полуоси 0у' как угодно близко, никогда, однако, ее не достигая, а ветви тех же кривых, расположенные выше оси x-ов, при возрастании х от 1 до |
||||||||||||||||||||||||||||||||||||
|
5. Понятие о значении логарифмических таблиц. Различные числа можно выражать как степени одного и того же числа, напр., как степени числа 10. Такие числа, как 10; 100; 1000... или 0,1; 0,01; 0,001 и т. п., выражаются, как степени 10 очень просто: 10 = 101 ; 100 = 102; 1000 = 103;... 0,1 = 10-1, 0,01 = 10-2 0,001 = 10-3 и т. п. Другие числа выразить степенью 10 затруднительно. Так, если требуется найти показатель степени, в которую нужно возвести
10, чтобы получить число 5, то мы можем только сказать, что искомый показатель больше 0, но меньше 1, так как 100 =1, что меньше 5, а 101 = 10, что больше 5; значит, показатель степени, в которую надо возвысить 10 для получения 5, должен быть некоторая положительная дробь меньшая 1. Мы можем даже сказать, что эта дробь больше 1/2 , но меньше 3/4, так как Но найти точно показатель х, чтобы 10x = 5, очень затруднительно. Есть отделы математики, в которых указываются способы, как можно для всякогo данного числа N найти такой показатель х, при котором степень 10x или в точности равняется N, или отличается от этого числа как угодно мало. Ученые, пользуясь этими способами, составили так называемые логарифмические таблицы, в которых помещены различные числа
и около каждого из этих чисел указан показатель степени (логарифм), в которую надо возвести 10, чтобы получить это число. Разъясним, для какой цели могут служить такие таблицы. |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Извлекать корень 5-й степени мы не умеем. В подобных случаях нам могут помочь логарифмические таблицы. Находим в этих таблицах число 40 и около него логарифм этого числа. Пусть это будет 1,6... Это значит, что |
||||||||||||||||||||||||||||||||||||
|
40 = 101,6... |
||||||||||||||||||||||||||||||||||||
|
и следовательно, |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Так как при извлечении корня из степени показатель подкоренного числа (какой бы он ни был) делится на показатель корня, то |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Теперь в тех же таблицах в столбце логарифмов находим 0,32 и около него соответствующее число, пусть это будет, положим, 2,09... Это и будет приближенное значение |
||||||||||||||||||||||||||||||||||||
|
Мы вскоре увидим, что логарифмические таблицы во многих случаях позволяют производить такие действия над числами, которые без таблиц мы или совсем не могли бы выполнить (как в примере, только что указанном), или на выполнение которых потребовалось бы очень много времени. Теперь нам предстоит ознакомиться, во-первых, с тем, как при совершении какого-либо действия над данными числами можно найти логарифм искомого числа при помощи логарифмов этих данных чисел (взятых из таблиц) и, во-вторых, как найдя такой логарифм, отыскать по нему в таблицах искомое число. |
||||||||||||||||||||||||||||||||||||
|
6. Нахождение логарифма произведения, частного, степени и корня. |
||||||||||||||||||||||||||||||||||||
|
а) Пусть требуется выполнить умножение: 378 . 45,2 |
||||||||||||||||||||||||||||||||||||
|
Попробуем выполнить это действие посредством логарифмов. Найдем в таблицах логарифмы чисел 378 и 45,2. Пусть они будут: 2,5775 и 1,6551 (по основанию 10). Это значит, что |
||||||||||||||||||||||||||||||||||||
|
378 = 102,5775 и 45,2 = 101,6551 |
||||||||||||||||||||||||||||||||||||
|
и следовательно, |
||||||||||||||||||||||||||||||||||||
|
378 . 45,2 = 102,5775 . 101,6551 |
||||||||||||||||||||||||||||||||||||
|
Так как при умножении степеней одного и того же числа показатели этих степеней складываются (какие бы ни были эти показатели), то |
||||||||||||||||||||||||||||||||||||
|
378 . 45,2 = 102,5775 + 1,6551= 104,2326 |
||||||||||||||||||||||||||||||||||||
|
Значит, логарифм произведения 378 . 45,2 есть число 4,2326, получившееся от сложения логарифмов данных сомножителей (по этому логарифму в таблицах найдем и само произведение). |
||||||||||||||||||||||||||||||||||||
|
Положим вообще, что N1 и N2 будут два числа, произведение которых требуется вычислить. Пусть мы нашли в таблицах логарифмы этих чисел х1 и х2. Основание этих логарифмов может быть число 10, но может быть и какое-нибудь другое число, которое мы обозначим а. Тогда мы будем иметь равенства: |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Отсюда видно, что log (N1N2) = x1 + x2 Но x1 - это log N1 , а х2 - это log N2; значит: |
||||||||||||||||||||||||||||||||||||
|
log (N1N2) = log N1 + log N2 , |
||||||||||||||||||||||||||||||||||||
|
т. е. логарифм произведения (по какому угодно основанию) равен сумме логарифмов сомножителей (взятых по тому же основанию). |
||||||||||||||||||||||||||||||||||||
|
Заключение это остается верным и тогда, когда сомножителей будет более 2, так как при умножении степеней одного и того же числа показатели их складываются и тогда, когда, этих степеней будет более 2. |
||||||||||||||||||||||||||||||||||||
|
б) Положим, надо выполнить деление: | ||||||||||||||||||||||||||||||||||||
|
5637 : 26,3. |
||||||||||||||||||||||||||||||||||||
Найдем в таблицах логарифмы этих чисел (напр, по основанию 10). | ||||||||||||||||||||||||||||||||||||
|
5637 = 103,751 и 26,3 = 101,42 |
||||||||||||||||||||||||||||||||||||
|
Следовательно, 5637:26,3=103,751 :101,42 =103,751-1,42 =102,331 |
||||||||||||||||||||||||||||||||||||
|
Отсюда видно, что логарифм частного 5637:26,3 есть число 2,331, получившееся от вычитания логарифма делителя из логарифма делимого. |
||||||||||||||||||||||||||||||||||||
|
Вообще, если |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
и следовательно, |
||||||||||||||||||||||||||||||||||||
|
log(N1 : N2) = x1 - x2 =log N1 - log N2 |
||||||||||||||||||||||||||||||||||||
|
т. е. логарифм частного равен логарифму делимого без логарифма делителя. |
||||||||||||||||||||||||||||||||||||
|
Так как всякая дробь есть частное от деления числителя на знаменатель, то логарифм дроби равен логарифму числителя без логарифма знаменателя. |
||||||||||||||||||||||||||||||||||||
|
Напр.: log 2/3 = log 2 — log 3; Следствие : Поскольку loga1 = 0, то
Таким образом
Логарифмы двух взаимообратных чисел по одному и тому же основанию отличаются друг от друга только знаком. |
||||||||||||||||||||||||||||||||||||
|
в) Если N = ax, то Nn = (ax)n= anx; следовательно: log (Nn) = nx = n log N, т. e. логарифм степени равен показателю этой степени, умноженному на логарифм возводимого в степень числа. |
||||||||||||||||||||||||||||||||||||
|
Напр.: log (15,3)2 = 2 log 15,3; |
||||||||||||||||||||||||||||||||||||
|
г) Так как
т. e. логарифм корня равен логарифму подкоренного числа, деленному на показатель корня. |
||||||||||||||||||||||||||||||||||||
|
д) Переход от одного основания логарифмов к другому.
Но по правилу о логарифме степени
Следовательно, loga b • logcа = logcb, откуда вытекает формула
Если вместо основания с возьмем число b, то
Пусть, например, нам известно, что log102 |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
7. Логарифмирование алгебраического выражения. Логарифмировать алгебраическое выражение значит выразить логарифм его посредством логарифмов отдельных чисел, составляющих это выражение. Выводы предыдущего параграфа позволяют это сделать в применении к произведению, частному, степени и дроби. |
||||||||||||||||||||||||||||||||||||
1) 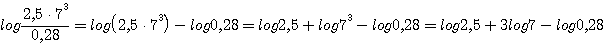 |
||||||||||||||||||||||||||||||||||||
2) 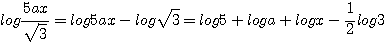 |
||||||||||||||||||||||||||||||||||||
3)  |
||||||||||||||||||||||||||||||||||||
|
8. Замечания. а) Если в выражении, которое требуется вычислить, встречается сумма или разность чисел, то их надо находить без помощи таблиц обыкновенным сложением или вычитанием. Напр.: log (35 +7,24)5 = 5 log (35 + 7,24) = 5 log 42,24. б) Умея логарифмировать выражения, мы можем, обратно, по данному результату логарифмирования найти то выражение, от которого получился этот результат; так, если log х = log a + log b — 3 log с, то легко сообразить, что Операция обратная логарифмированию , называется потенцированием
|
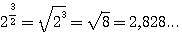
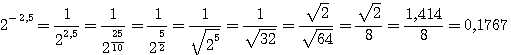
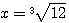
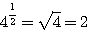 ;
;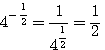
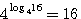
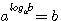 - логарифм числа b по основанию а есть показатель степени, в которую нужно возвести число а, чтобы получить число b.
- логарифм числа b по основанию а есть показатель степени, в которую нужно возвести число а, чтобы получить число b. ; 3) у = 10х,
; 3) у = 10х,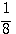
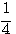
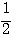
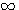
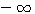
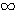
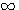
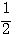
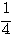
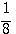
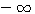
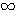
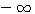
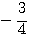
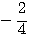
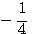
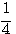
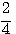
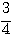

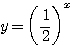 ; у = 10х, только они расположены симметрично с этими кривыми относительно биссектрисы угла хОу.
; у = 10х, только они расположены симметрично с этими кривыми относительно биссектрисы угла хОу.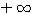 , поднимаются все выше и выше неограниченно.
, поднимаются все выше и выше неограниченно. 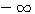 до 0; с возрастанием числа от 1 до
до 0; с возрастанием числа от 1 до 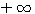 логарифм его возрастает от 1 до
логарифм его возрастает от 1 до 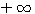 Из этого между прочим следует, что большему числу соответствует больший логарифм (при основании, меньшем 1 (a <1) , заключение было бы обратное).
Из этого между прочим следует, что большему числу соответствует больший логарифм (при основании, меньшем 1 (a <1) , заключение было бы обратное).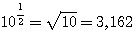 , что меньше 5, a
, что меньше 5, a 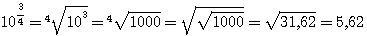 , что больше 5.
, что больше 5.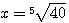
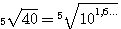
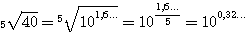
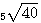
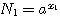 ;
; 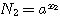 ; следовательно
; следовательно 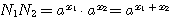
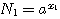 ;
; 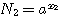 ; то
; то 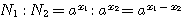
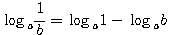
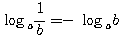
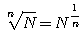 то, применяя правило о логарифме степени, получим:
то, применяя правило о логарифме степени, получим: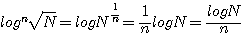
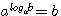 , ( предполагая, что a>0, b>0)
, ( предполагая, что a>0, b>0)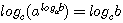
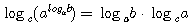
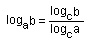
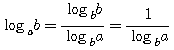 , таким образом
, таким образом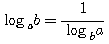
 0,3010 ; log103
0,3010 ; log103