Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§9. УГОЛ. ДЕЙСТВИЯ НАД УГЛАМИ.
1. Определение угла.
Если на классной доске или на странице тетради возьмём точку и из неё проведём два луча (черт. 39), то получим угол.
Углом называется фигура, образованная двумя лучами, выходящими из одной точки.
Угол обозначается значком / .
Точка, из которой выходят лучи, называется вершиной угла, а лучи, образующие угол, называются сторонами угла (черт. 39).

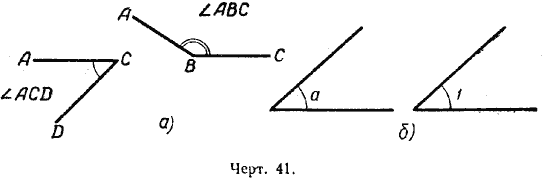
Угол обозначается или одной большой буквой, поставленной у вершины угла, например А или В (черт. 40), или тремя буквами, из которых одна ставится при вершине угла, а две другие — у каких-нибудь точек сторон, например / АВС или / АСD (черт. 41, а). Буква, стоящая при вершине угла, всегда записывается между двумя другими буквами. Иногда угол обозначают одной малой буквой или цифрой, поставленной внутри угла (черт. 41, б).
Вырежем из листа бумаги начерченный на ней угол, получим модель угла (черт. 42, а). Моделью угла оказывается часть листа бумаги, ограниченная сторонами угла (на чертеже она заштрихована).
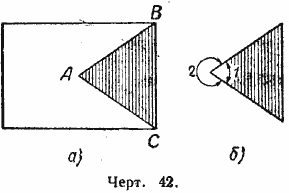
Оставшаяся часть листа тоже является моделью угла, но уже -другого. Поэтому нужно считать, что на чертеже изображены два угла. На модели ясно, какой угол взят; чтобы это было ясно и на чертеже, следует взятый угол как-нибудь отметить, например дугой и номером, как это показано на чертеже 42, б.
Стороны угла, начерченного на листе бумаги, разделяют лист бумаги на две части (черт. 42, а); точно так же стороны угла, взятого на плоскости, разделяют плоскость на две области.
Для каждого угла одна из областей называется внутренней. Внутренней областью для / 1 является область, заштрихованная на чертеже, для / 2 внутренняя область оставлена незаштрихованной (черт. 42, б). В дальнейшем будем рассматривать угол вместе с его внутренней областью.
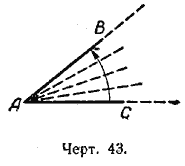
Образование угла можно представить себе иначе. Если мы возьмём луч АС (черт. 43) и повернём его вокруг точки А, то начальное (АС) и конечное (АВ) положения луча образуют угол.
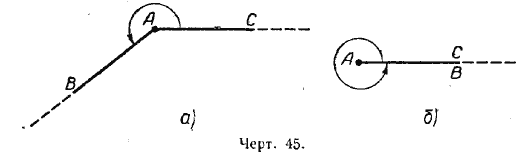
Продолжая вращать луч в том же направлении, мы будем получать всё новые и новые углы. Может наступить такой момент, когда оба луча будут составлять прямую линию (черт. 44). Такой угол называется развёрнутым углом.
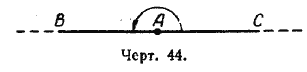
Если будем продолжать вращение луча и дальше, снова будем получать новые углы (черт. 45, а), и, наконец, луч может занять своё прежнее положение (черт. 45, б). В этом случае угол будет называться полным углом.
2. Сравнение углов по величине.
Начертим на листе бумаги какой-нибудь угол ABC и переведём его с помощью копировальной бумаги на другой лист, получим угол DEF (черт. 46). Вырежем оба эти угла и затем наложим их друг на друга, например угол DEF на угол ABC, так, чтобы:
1) вершина Е совпала с вершиной В,
2) сторона EF пошла по стороне ВС и
3) внутренняя область угла DEF легла на внутреннюю область угла ABC.
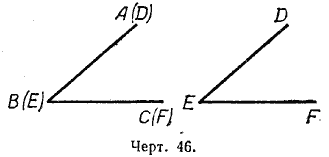
Выполнив наложение, мы увидим, что сторона ED пойдёт по стороне ВА, углы ABC и DEF совместятся, т. е. они будут равны.
Углы называются равными, если их можно совместить наложением. Равенство углов обозначается так: / ABC = / DEF.
Развёрнутые углы при наложении могут быть совмещены. Отсюда, все развёрнутые углы равны между собой.
Полные углы при наложении также могут быть совмещены. Следовательно, все полные углы равны между собой.
Рассмотрим теперь чертёж 47.
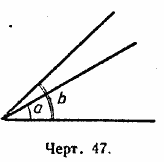
Углы а и b наложены друг на друга, причём внутренняя область угла а занимает только часть внутренней области угла b.
Поэтому считается, что угол а меньше угла b, а угол b больше угла а:
/ a < / b, / b > / a.
Вообще, из двух углов тот считается меньшим, внутренняя область которого при наложении углов друг на друга занимает только часть внутренней области другого угла.
На чертежах мы вынуждены стороны угла изображать в виде отрезков, но стороны угла — это лучи, а лучи бесконечны, поэтому мы стороны каждого угла должны представлять себе продолженными бесконечно. Значит, от того, изобразим ли стороны данного угла длинными или короткими отрезками, величина угла не изменится, т. е. величина угла не зависит от длины его сторон.
3. Действия над углами. Биссектриса угла.
Если один угол приложить к другому так, что они будут иметь общую вершину и сторону, а внутренние области углов не будут налегать друг на друга, то полученный таким образом угол будет называться суммой этих углов (черт. 48).
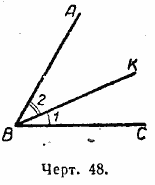
/ ABC = / 1 + / 2 или / ABC = / KBC + / ABK.
/ KBC является разностью углов ABC и АВК:
/ KBC = / ABC — / ABK. Точно так же / ABK = / ABC — / KBC.
Можно получить сумму не только двух, но и нескольких углов (черт. 49):
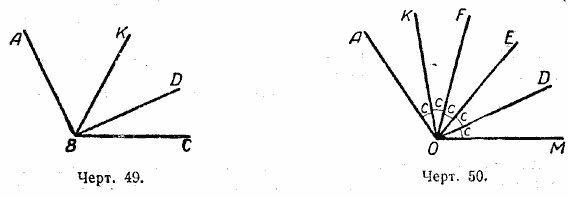
/ ABC = / DBC + / KBD + / ABK.
При сложении углов выполняются переместительный и сочетательный законы, как и при сложении отрезков.
Если взять сумму нескольких равных углов, т. е. один и тот же угол повторить слагаемым несколько раз (черт. 50), то полученный угол будет результатом умножения угла не целое число: / AOM = 5 / c. Следовательно, / c будет равен 1/5 / АОМ;
/ EOM = 2/5 / АОМ; / FOM = 3/5 / AOM; / KOM = 4/5 / АОМ.
Луч, делящий угол пополам, называется биссектрисой угла (черт. 51).

Полный угол равен сумме двух развёрнутых углов (черт. 52), а развёрнутый угол равен половине полного угла.
4. Прямой угол.
Возьмём лист бумаги и на одной стороне его, как показано на чертеже 53, обозначим точку В, которую примем за вершину развёрнутого угла; стороны этого угла обозначим через BD и ВС.
Если лист бумаги согнём так, чтобы сгиб прошёл через точку В, а лучи BD и ВС совпали, то развёрнутый угол разделится на два равных угла. Каждый из них будет составлять половину развёрнутого угла. Угол, равный половине развёрнутого угла, называется прямым углом. / ABC = / ABD (черт. 53).
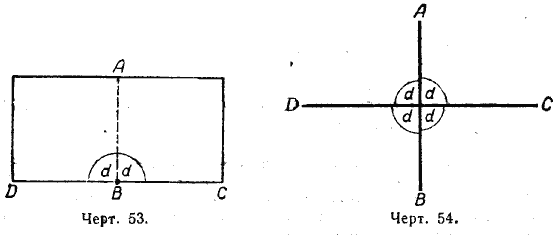
Так как все развёрнутые углы равны между собой, то и все прямые углы, как половины равных углов, также равны между собой. Величина прямого угла обозначается буквой d; / ABC = d; / ABD = d. Развёрнутый угол равен 2d. Полный угол равен 4d (черт. 54).