ГЛАВА IV.

ЧЕТЫРЁХУГОЛЬНИКИ.

§ 46. ЧАСТНЫЕ ВИДЫ ПАРАЛЛЕЛОГРАММОВ.

1. Прямоугольник.

Построим прямой угол А. Обозначим на его сторонах две произвольные точки В и С (черт. 235). Через точку В проведём прямую, параллельную АС, а через точку С проведём прямую, параллельную АВ.

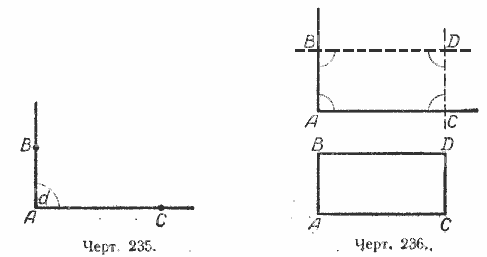
Точку пересечения этих прямых обозначим буквой D (черт.236). Мы получили параллелограмм АВDС, в котором /  А = d. Нетрудно доказать, что в этом параллелограмме все внутренние углы будут прямые.

В самом деле, /  В + /  А =2d, как углы внутренние односторонние при параллельных прямых АС и ВD и секущей AB. Но /  А = d, следовательно, и /  В = d. Кроме того,
/  A = /  D  и  /  В = /  С, как противоположные углы параллелограмма. Таким образом, все углы этого параллелограмма прямые.

Параллелограмм, у которого все углы прямые, называется прямоугольником.

2. Свойства прямоугольника.

Так как прямоугольник есть параллелограмм, то он обладает всеми его свойствами (§ 43).

1. Диагональ прямоугольника делит его на два равных треугольника.

2. Диагонали прямоугольника в точке их пересечения делятся пополам.

3. Противоположные стороны прямоугольника равны между собой, равны также и противоположные углы его.

Кроме этих свойств, прямоугольник обладает еще следующим свойством:
Диагонали прямоугольника равны.

Докажем это свойство. Возьмём прямоугольник АВСD, проведём в нём две диагонали (черт. 237) АС и ВD и докажем, что они равны между собой.

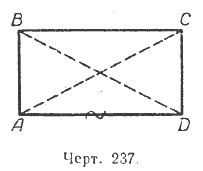
Сравним два треугольника АВD и АСD. Сторона АD у них общая и АВ = DС. Кроме того, они прямоугольные. Следовательно, они равны между собой, поэтому АС = ВD.

Упражнение. Докажите, что если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.

Этим свойством прямоугольника пользуются в столярных и слесарных мастерских для проверки, насколько точно сделаны те или иные детали или предметы, которые должны иметь прямоугольную форму, например: крышка стола, дно или боковая стенка ящика, рамка для картины и т. д.

Если противоположные стороны четырёхугольника попарно равны и равны его диагонали, то он должен быть прямоугольником. В противном же случае он не будет иметь форму прямоугольника и потребует соответствующего исправления.

3. Построение прямой, все точки которой находятся
на данном расстоянии l от данной прямой.

Если через точку А, находящуюся на расстоянии l от данной прямой МС, провести прямую, параллельную МС, то любая точка этой прямой будет находиться на расстоянии l от прямой МС (черт. 238).

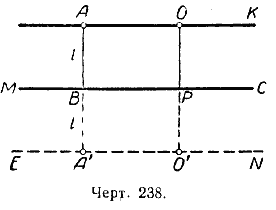
Если АВ = l и ОР_|_МС, то ОР = АВ = l (как противоположные стороны прямоугольника).

Кроме прямой АК, по другую сторону МС можно построить ещё прямую ЕN, обладающую тем же свойством: ВА' = РО' = l. Точки плоскости, не лежащие на прямых
АК и ЕN, этим свойством не обладают.

Прямые АК и ЕN являются геометрическим местом точек, отстоящих от данной прямой МС на расстоянии l.

Эти две прямые симметричны относительно данной прямой.

4. Ромб.

Построим угол и на его сторонах отложим от вершины А равные отрезки АВ = АС (черт. 239).

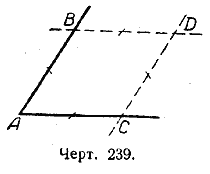
Через точку В проведём прямую, параллельную АС; через точку С проведём прямую, параллельную АВ. Точку пересечения этих прямых обозначим через D. Мы получили параллелограмм АВDС, причём ВD = АС, СD = АВ, как противоположные стороны параллелограмма. Отсюда: ВD = АС = АВ = DС.

Параллелограмм, у которого все стороны равны, называется ромбом.

5. Свойства ромба.

Так как ромб есть параллелограмм, то он обладает всеми его свойствами.

 1. Диагональ ромба делит его на два равных треугольника.
 2. Диагонали ромба в точке их пересечения делятся пополам.
 3. Противоположные стороны ромба равны между собой, равны и противоположные углы его.

Кроме того, ромб обладает ещё следующими свойствами:

 а) диагонали ромба взаимно перпендикулярны;
 б) диагональ ромба делит угол его пополам.

В ромбе АВСD проведём две диагонали АС и ВD (черт. 240), пересекающиеся в точке О, и докажем, что АС_|_ ВD, а диагональ АС делит угол С пополам.

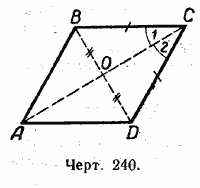
В равнобедренном треугольнике ВСD отрезок СD является медианой, а следовательно, и высотой, и биссектрисой угла С. Отсюда АС _|_ ВD и /  1 = /  2 . Так же доказывается, что диагональ АС делит пополам угол А, а диагональ ВD делит пополам углы   В и D.

6. Квадрат.

Построим прямой угол и на его сторонах отложим равные отрезки АВ и АС (черт. 241).

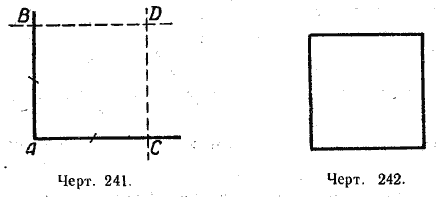
Через точки В и С проведём прямые, параллельные сторонам АС и А В. Точку пересечения их обозначим через О. Мы получили четырёхугольник, в котором:

 а) противоположные стороны попарно параллельны, следовательно, это параллелограмм;
 б) все углы прямые, следовательно, это прямоугольник;
 в) все стороны равны, следовательно, это ромб.

Прямоугольник, в котором все стороны равны,  называется квадратом
(черт. 242).

Может быть дано и такое определение квадрата: ромб, у которого все углы прямые, называется квадратом.

7. Свойства квадрата.

Так как квадрат является и параллелограммом, и прямоугольником,  и ромбом, то он обладает всеми их свойствами.

1. а) Диагональ квадрата делит его на два равных треугольника.
    б) Диагонали квадрата в точке их пересечения делятся пополам.
    в) Противоположные стороны квадрата равны между собой, равны и противоположные углы его. (Свойства параллелограмма.)

2. Диагонали квадрата равны.  (Свойство прямоугольника.)

3. а) Диагонали квадрата взаимно перпендикулярны.
    б) Диагональ квадрата делит его угол пополам. (Свойства ромба.)

8. Симметрия прямоугольника, ромба и квадрата.

Так как прямоугольник, ромб и квадрат являются параллелограммами, то точка пересечения диагоналей этих фигур является также их центром симметрии.

Прямоугольник, ромб и квадрат, кроме того, имеют ещё oси симметрии. В прямоугольнике осями симметрии являются прямые, проходящие через середины противоположных сторон (черт. 243).

В ромбе осями симметрии являются две его диагонали (черт. 244).

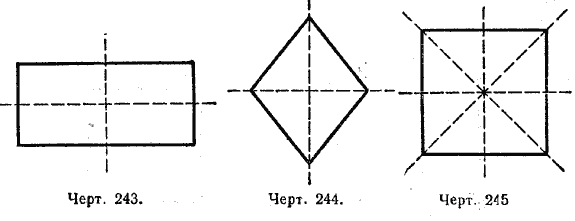
Квадрат имеет четыре оси симметрии (черт. 245), которые указаны для прямоугольника и ромба.

Упражнения.

1. Перечислите изученные свойства параллелограмма.

2. Перечислите изученные свойства прямоугольника.

3. Перечислите изученные свойства ромба.

4. Диагонали четырёхугольника взаимно перпендикулярны. Значит ли, что этот четырёхугольник — ромб?  При каком дополнительном условии он будет ромбом?

5. Построить ромб по данной стороне н прилежащему углу.

6. Построить ромб по двум его диагоналям.

7. Построить квадрат по данной его стороне.

8. Построить квадрат по его диагонали.

9. Приложить двустороннюю линейку сначала к одной стороне произвольного угла А, а затем к другой стороне и провести две прямые, параллельные сторонам этого угла (черт. 246).

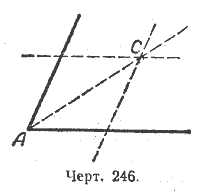
Точку С пересечения этих двух прямых соединить с вершиной угла и доказать, что прямая АС разделит /  А пополам.

10. В следующих задачах дополнить условие недостающими данными, чтобы решение было единственным:

 а) Построить ромб по данной его стороне;
 б) Построить прямоугольник по данной его стороне;
 в) Построить ромб по данному углу;
 г) Построить параллелограмм по данной его стороне.

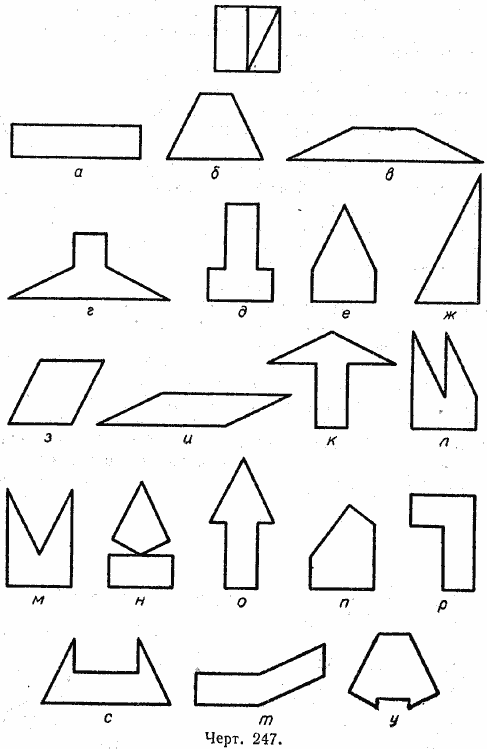
11. Вырезать квадрат, разрезать его на части, как показано на чертеже 247, и составить из них фигуры, приведённые на этом чертеже.