ГЛАВА VI.

ПРЯМАЯ ПРИЗМА. ПОВЕРХНОСТЬ И ОБЪЁМ ПРЯМОЙ ПРИЗМЫ.

§ 63. КУБ.

1. Построение модели куба.

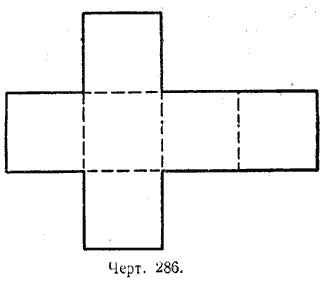
На чертеже 286 изображена выкройка, или, как её принято называть, развёртка геометрического тела. Она состоит из шести равных квадратов. Если эту развёртку согнуть надлежащим образом по указанным на чертеже пунктирным линиям, то мы получим геометрическое тело, называемое кубом.

Под номером 287 дан чертёж куба, а под номером 288 дан рисунок куба. Куб ограничен шестью равными квадратами, которые называются его гранями.

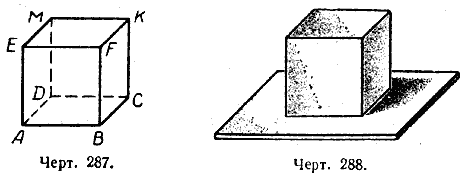
На рисунке видны только три его грани, а на чертеже можно видеть все шесть граней. Любые две противоположные грани куба называются его основаниями, тогда остальные четыре его грани называются боковыми гранями; отрезки, которые получаются при пересечении граней куба, называются его рёбрами. У куба 12 рёбер. Все они равны между собой.При пересечении трёх граней куба образуются точки, которые называются его в е р ш и н а м и. У куба 8 вершин.

2. Взаимное положение рёбер и граней куба.

Противоположные грани куба параллельны. Плоскости, в которых лежат эти грани, не пересекаются, т. е. не имеют общих точек. Параллельные плоскости мы наблюдаем на многих окружающих нас предметах; например, плоскости пола и потолка в комнате параллельны.
В кубе можно наблюдать и пересекающиеся плоскости. Пересекаясь, плоскости образуют двугранные углы. Модель двугранных углов можно получить, сгибая лист картона или бумаги по прямой линии.

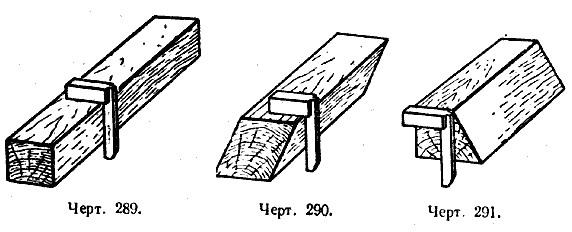
Двугранные углы можно получить острые, прямые и тупые. Грани куба пересекаются под прямым углом. Под прямым углом пересекаются также стены в комнате, стены и потолок, стены и пол. Плоскости, пересекающиеся под прямым углом, называются перпендикулярными. Перпендикулярность плоскостей проверяется с помощью угольника. На чертеже 289 плоскости при пересечении образуют прямой угол. На чертеже 290 и на чертеже 291 показаны плоскости, которые при пересечении не образуют прямого угла; в первом случае они пересекаются под острым углом, во втором случае — под   тупым.

Рёбра куба, находящиеся на одной грани (черт. 287), или пересекаются под прямым углом (ЕА _|_ АВ, КС _|_ ВС и т. д.), или параллельны (ЕF || АВ, ВС || КF и т. д.).

3. Скрещивающиеся прямые.

Рёбра куба, например КС и АВ (черт. 287), не параллельны, но и не пересекутся, сколько бы их ни продолжать. Прямые, которые не параллельны и не пересекаются, называются скрещивающимися. Легко получить модели скрещивающихся прямых. Например, две иглы, из которых одна положена на стол, а другая воткнута в стол так, что не пересекает первую, представляют собой модель двух скрещивающихся прямых (черт. 292). Эти две прямые не пересекаются и не параллельны; легко убедиться, что через них нельзя провести плоскость.

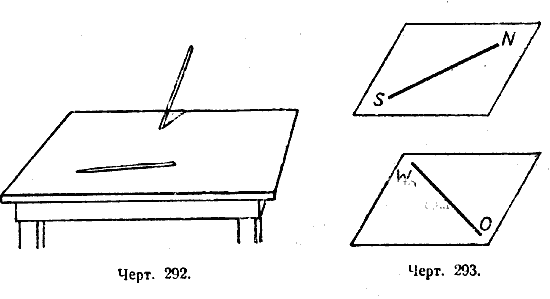
Точно так же, если взять две дощечки, поместить их параллельно друг другу и затем на одну из них положить палочку в направлении, например, с юга на север, а на другую — в направлении с запада на восток, то эти две палочки образуют модель скрещивающихся прямых (черт. 293).

Эти две прямые тоже не пересекаются, не параллельны, и через них также нельзя провести плоскость.

Найдите модели скрещивающихся прямых на окружающих предметах, например, в классной комнате.

4. Прямая, перпендикулярная к плоскости.

Рассматривая куб (черт. 287), заметим, что ребро FВ образует прямые углы с рёбрами ВС и АВ, лежащими на нижнем основании куба. Это же ребро FВ образует прямые углы с любой прямой, проведённой в плоскости основания куба через точку В. Ребро FВ является перпендикуляром к плоскости основания куба.

Перпендикуляром к плоскости называется прямая, которая пересекает плоскость в какой-нибудь точке и перпендикулярна к любой прямой, проведённой в этой плоскости через ту же точку.

Чтобы провести перпендикуляр к плоскости, берут два чертёжных треугольника и ставят их так, чтобы два катета лежали на плоскости, как показано на чертеже 294, а другую пару катетов совмещают. Эти два катета и образуют перпендикуляр к данной плоскости.

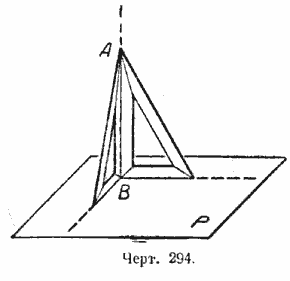
На чертеже 294 прямая АВ перпендикулярна к плоскости Р.

Перпендикулярность прямой АВ к плоскости Р легко проверить: для этого надо взять ещё один чертёжный треугольник и несколько раз в различных положениях приложить его к двум первым треугольникам так, чтобы его катет всякий раз совмещался с катетом АВ. Тогда другой катет третьего треугольника всё время будет находиться в плоскости Р. Значит, можно считать проверенным, что прямая АВ образует прямые углы с любой прямой, проведённой на плоскости через её основание, т. е. является перпендикуляром к плоскости.

Таким образом, мы приходим к выводу: если прямая, пересекающая плоскость в какой-нибудь точке О, перпендикулярна к двум прямым, проведённым на плоскости через точку О, то эта прямая перпендикулярна к плоскости.

Этот вывод является признаком перпендикулярности прямой к плоскости.

Через любую произвольно взятую точку можно провести перпендикуляр к данной плоскости, но только один.

Длина перпендикуляра, опущенного из какой-нибудь точки на плоскость, называется расстоянием от этой точки до плоскости.

5. Площадь поверхности куба.

Чтобы вычислить площадь поверхности куба, достаточно вычислить площадь одной его грани и полученное число помножить на 6. Если ребро куба обозначить через а, то площадь поверхности одной его грани будет равна а², а площадь всей поверхности куба (полная поверхность) составит 6а².

S = 6а², где S — площадь полной поверхности куба.

Площадь поверхности его оснований составит 2а². Площадь поверхности боковых его граней составит 4а².

Упражнения.

1. Ребро куба равно 8 см (10 см, 12 см, 20 см). Вычислить площадь всей его поверхности; площадь оснований; площадь его боковой поверхности.

2. Площадь полной поверхности куба равна 150 кв. см (600 кв. см, 216 кв. см, 864 кв. см). Вычислить длину его ребра.

3. Площадь боковой поверхности куба равна 100 кв. см (64 кв. см, 324 кв. см, 576 кв. см). Вычислить площадь его полной поверхности.

4. Сделать из плотной бумаги модель куба, ребро которого равно 8 см.

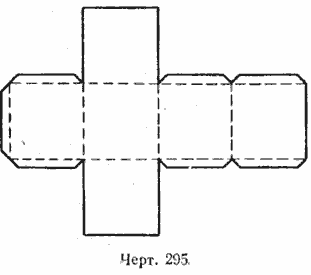
Указание. Для того чтобы полученное геометрическое тело сохраняло свою форму, у развёртки куба необходимо сделать небольшие закраины (черт. 295). Если их подклеить, они составят каркас, который придаст необходимую жёсткость модели.

5. Сколько потребуется белил для окраски с обеих сторон бака (без крышки), имеющего форму куба с ребром в 80 см, если на окраску 1 кв.м требуется белил 0,25 кг?