ГЛАВА VII.

ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.

§ 71. ЗАВИСИМОСТЬ МЕЖДУ ХОРДАМИ И ДУГАМИ.

Докажем ряд теорем, устанавливающих зависимость между хордами и их дугами в одной и той же окружности или в равных окружностях.

При этом будем иметь в виду дуги, меньшие полуокружности.

Теорема 1. Равные дуги стя гиваются равными хордами.

Пусть дуга АВ равна дуге СК. Требуется доказать, что и хорда АВ равна хорде СК  (черт. 314).

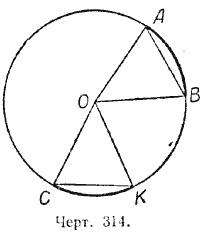
Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны, так как имеют по две соответственно равные стороны (радиусы одной окружности) и по равному углу, заключённому между этими сторонами (эти углы равны, как центральные, соответствующие равным дугам). Следовательно, АВ = СК.

Теорема 2 (обратная). Равные хорды стягивают равные дуги.

Пусть хорда АВ равна хорде СК. Требуется доказать, что дуга АВ равна дуге СК (черт. 314).

Доказательство. Соединим концы хорд с центром окружности— точкой О. Полученные треугольники АОВ и КОС равны по трём соответственно равным сторонам. Следовательно, равны углы АОВ и СОК; но углы эти центральные, соответствующие дугам АВ и СК; из равенства этих углов следует равенство дуг: АВ = СК.

Теорема 3. Большая дуга стягивается и большей хордой.

Пусть дуга АВ больше дуги СК (черт. 315).

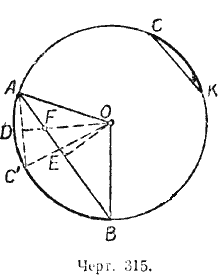
Требуется доказать, что хорда АВ больше хорды СК.

Доказательство. Передвинем по окружности дугу СК так, чтобы точка К совместилась с точкой А, тогда точка С займёт положение С' на дуге АВ между точками A и В, дуга СК примет положение дуги АС', а хорда СК примет положение хорды АС'. Проведём радиусы в точки A, В и С'. Опустим из центра О перпендикуляры ОЕ и ОD на хорды АВ и АС'. В треугольнике ОFE отрезок ОЕ - катет , а отрезок ОF — гипотенуза, поэтому OF > ОЕ, а потому и OD > OE.

Рассмотрим теперь треугольники ОАD и ОАЕ. В этих треугольниках гипотенуза ОА общая, а катет ОЕ меньше катета ОD, тогда по следствию из теоремы Пифагора (§ 58) катет АЕ больше катета АD. Но эти катеты составляют половины хорд АВ и АС', значит, и хорда АВ больше хорды АС'. Вследствие равенства хорд АС' и СК получаем
АВ > СК.

Теорема 4 (обратная). Большая хорда стягивает и большую дугу.

Пусть хорда А В больше хорды СК.

Требуется доказать, что дуга АВ больше дуги СК (черт. 315). Между дугами АВ и СК может существовать только одно из трёх следующих соотношений:

АВ < СК;
АВ = СК;
АВ > СК.

Но дуга AВ не может быть меньше дуги СК, так как тогда по прямой теореме хорда АВ была бы меньше хорды СК, а это противоречит условию теоремы.

Дуга АВ не может быть равна дуге СК, так как тогда хорда АВ равнялась бы хорде СК, а это тоже противоречит условию. Следовательно, АВ > СК.