ГЛАВА VIII.
ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ. ПОДОБИЕ ФИГУР.
§ 84. ПОСТРОЕНИЕ ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКОВ.
Теорема. Если две прямые пересень тремя параллельными, прямыми, то отношение двух отрезков, получившихся на одной прямой, равно отношению двух соответствующих отрезков другой прямой.
Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (черт. 354).
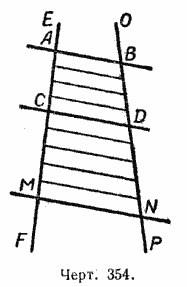
Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.
AC/CM = BD/DN
Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.
Например, р = 4 см. и q = 5 см.
Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на чертеже 354.
Тогда на прямой ОР отложатся равные между собой отрезки (§ 47), при этом на отрезке BD их будет 4, а на отрезке DN — 5.
Отношение АС к СМ равно 4/5 , точно так же и отношение ВD к DN равно 4/5.
Отсюда AC/CM = BD/DN.
Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. AC/AM = BD/BN,
так как AC/AM = 4/9 и BD/BN = 4/9
Теорема будет справедлива и при любых других целых значениях р и q.
Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.
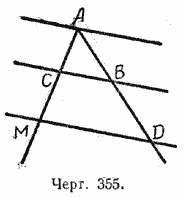
Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых (черт. 355). Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток (черт. 356). Справедливость этих предложений доказать самостоятельно.