ГЛАВА VIII.
ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ. ПОДОБИЕ ФИГУР.
§ 92. ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ ФИГУР.
1. Отношение площадей квадратов.
Рассмотрим отношение площадей двух квадратов. Если сторону одного квадрата обозначим через т, а сторону другого — через п, то площади будут соответственно равны
т2 и п2 (черт. 379).
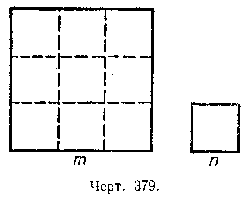
Обозначив площадь первого квадрата через S, а площадь второго через S', получим: S/S' = m2/n2 , т. е. площади квадратов относятся как квадраты их сторон.
Полученную формулу можно преобразовать так: S/S' = ( m/n)2 .
Значит, можно сказать, что отношение площадей двух квадратов равно квадрату отношения их сторон.
На чертеже 379 отношение сторон квадратов равно 3, отношение их площадей равно
32 = 9.
2. Отношение площадей двух подобных треугольников.
Пусть /\ AВС 
/\ A'В'С' (черт. 380). Из подобия треугольников следует, что
/
A = /
A' , /
B = /
B' и /
С = /
С' . Кроме того, AB/A'B' = BC/B'C' = AC/A'C'.
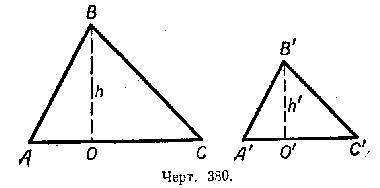
В этих треугольниках из вершин В и В' проведём высоты и обозначим их через h и h'. Площадь первого треугольника будет равна AC•h/2, а площадь второго треугольника A'C'•h'/2.
Обозначив площадь первого треугольника через S, а площадь второго — через S' получим: S/S' = AC•h/A'C'•h' или S/S' = AC/A'C' • h/h'
Из подобия треугольников АВО и А'В'О' (они подобны, потому что прямоугольные, и, кроме того, имеют по равному острому углу, а именно /
A = /
A' ) следует:
h/h' = AB/A'B' . Но AB/A'B' = AC/A'C' . Следовательно, h/h' = AC/A'C'. Заменив в формуле S/S' = AC/A'C' • h/h' отношение h/h' равным ему отношением AC/A'C' , получим:
S/S' = AC/A'C' • AC/A'C' , или 
.
Итак, площади подобных треугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать так: S/S' = (AC/A'C' )2.
Значит, можно сказать, что отношение площадей двух подобных треугольников равно квадрату отношения их сходственных сторон.
3. Отношение площадей подобных многоугольников.
Пусть ABCDE и A'B'C'D'E' — подобные многоугольники (черт. 381).
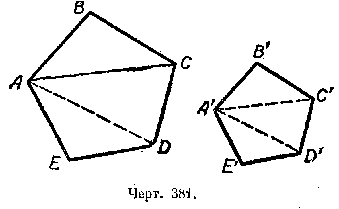
Известно, что /\ AВС /\ A'В'С'; /\ ACD /\ A'C'D' и /\ ADE /\ A'D'E' (§90).
Кроме того,
; 
Так как вторые отнoшения этих пропорций равны, что вытекает из подобия многоугольников, то 
Используя свойство ряда равных отношений получим:
, или 
где S и S' — площади данных подобных многоугольников.
Следовательно, площади подобных многоугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать к такому виду: S/S' = (AВ/A'В' )2
Упражнения.
1. Сторона первого квадрата больше стороны второго квадрата в 2 раза (в 5 раз). Во сколько раз площадь первого квадрата больше площади второго квадрата?
2. Сторона первого квадрата составляет 1/3 (0,1) стороны второго квадрата. Какую часть площадь первого квадрата составляет от площади второго квадрата?
3. Коэффициент подобия в подобных многоугольниках равен 4 (1/5; 0,4; 2,5). Чему равно отношение их площадей?
4. Отношение площадей подобных многоугольников равно 36 (100; 0,09). Чему равно отношение сходственных сторон этих многоугольников?