ГЛАВА   X.

ВПИСАННЫЕ И ОПИСАННЫЕ МНОГОУГОЛЬНИКИ,

§ 106. СВОЙСТВА ВПИСАННЫХ И ОПИСАННЫХ ЧЕТЫРЁХУГОЛЬНИКОВ.

Теорема 1. Сумма противоположных углов вписанного четырёхугольника равна 180°.

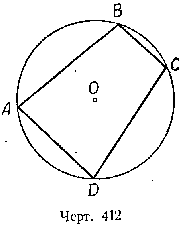
Пусть в окружность с центром О вписан четырёхугольник ABCD (черт. 412). Требуется доказать, что  /  А + /  С = 180° и /  В + /  D = 180°.

/   А, как вписанный в окружность О, измеряется  ¹/₂ BCD.
/   С, как вписанный в ту же окружность, измеряется  ¹/₂ BAD.

Следовательно, сумма углов А и С измеряется полусуммой дуг BCD и BAD в сумме же эти дуги составляют окружность, т. е. имеют  360°. 
Отсюда  /   А + /   С = 360° : 2 = 180°.

Аналогично доказывается, что и /   В + /   D = 180°. Однако это можно вывести и иным путём. Мы знаем, что сумма внутренних углов выпуклого четырёхугольника равна 360°. Сумма углов А и С равна 180°, значит, на сумму других двух углов четырёхугольника остаётся тоже 180° .

Теорема 2 (обратная). Если в четырёхугольнике сумма двух противоположных углов равна 180°, то около такого четырёхугольника можно описать окружность.

Пусть сумма противоположных углов четырёхугольника ABCD равна 180°, а именно
 /  А + /  С = 180° и /  В + /  D = 180°  (черт. 412).

Докажем, что около такого четырёхугольника можно описать окружность.

Доказательство. Через любые 3 вершины этого четырёхугольника можно провести окружность, например через точки А, В и С.   Где будет находиться точка D?

Точка D может занять только одно из следующих трёх положений: оказаться внутри круга, оказаться вне круга, оказаться на окружности круга.

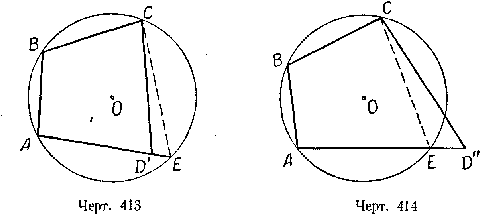
Допустим, что вершина окажется внутри круга и займёт положение D' (черт. 413). Тогда в четырёхугольнике ABCD' будем иметь:

/  В + /  D' = 2d.

Продолжив сторону AD' до пересечения с окружностью в точке Е и соединив точки Е и С, получим вписанный четырёхугольник АВСЕ, в котором по прямой теореме

/  B + /  Е = 2d.

Из этих двух равенств следует:

/  D' = 2d — /  B;
/  E = 2d — /  B;

откуда

/  D' =  / E,

но этого быть не может, так как /  D', как внешний относительно треугольника CD'E, должен быть больше угла Е. Поэтому точка D не может оказаться внутри круга.

Так же доказывается, что вершина D не может занять положение D" вне круга (черт. 414).

Остаётся признать, что вершина D должна лежать на окружности круга, т. е. совпасть с точкой Е, значит, около четырёхугольника ABCD    можно описать   окружность.

Следствия. 1. Вокруг всякого прямоугольника можно описать окружность.

2. Вокруг равнобедренной трапеции можно описать окружность.

В обоих случаях сумма противоположных углов равна    180°.

Теорема 3.   В   описанном  четырёхугольнике  суммы   противоположных сторон равны. Пусть  четырёхугольник   ABCD    описан   около   окружности (черт.  415), т. е. стороны его АВ, ВС, CD и DA — касательные к этой окружности.

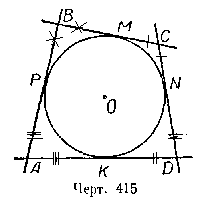
Требуется доказать, что АВ + CD =AD + ВС. Обозначим точки касания буквами М, N, К, Р,   На основании свойств касательных, проведённых к окружности из одной точки (§ 75),  имеем:

АР = АК;
ВР = ВМ;
DN = DK;
CN = СМ.

Сложим почленно эти равенства. Получим:

АР + ВР + DN + CN = АК + ВМ +DK + СМ,

т. е. АВ + CD = AD + ВС, что и требовалось доказать.

Упражнения.

1. Во вписанном четырёхугольнике два противоположных  угла относятся как 3 : 5,
а другие два относятся как 4 : 5. Определить величину этих   углов.

2.  В описанном четырёхугольнике сумма двух противоположных сторон равна 45 см. Остальные две  стороны относятся как 0,2 : 0,3. Найти длину этих сторон.