ГЛАВА V.

ЧЕТЫРЁХУГОЛЬНИКИ.

§ 17. Трапеция.

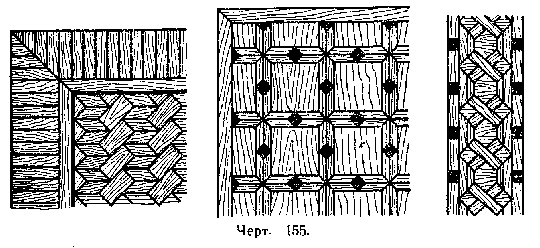
441. Указать, какими многоугольникамисоставлен рисунок паркета (черт. 155).

442. 1) Углы при основании трапеции равны 68° и 74°. Определить остальные углы трапеции.

2) Могут ли углы трапеции, взятые в последовательном порядке, относиться, как:
а) 6 : 3 : 4 : 2; б) 8 : 7 : 13 : 12?

443. Диагональ трапеции перпендикулярна к боковой стороне острый угол, лсмащий против этой диагонали, равен 40°. Найти остальные углы трапеции, если меньшее основание равно другой боковой стороне.

444. В трапеции ABCD меньшее основание ВС равно 4 см. Через вершину В проведена прямая, параллельная боковой стороне. Периметр образовавшегося треугольника равен 12 см. Найти периметр трапеции.

445. 1) В равнобедренной трапеции один из углов равен 60°, боковая сторона равна
24 см, а сумма оснований равна 43 см. Найти основания трапеции.

2) Найти периметр равнобедренной трапеции, если известно, что её острый угол равен 60°, а основания равны 15 сми 49 см.

446. Доказать, что если боковая сторона трапеции равна меньшему основанию, то диагональ, соединяющая их концы, является биссектрисой угла, прилсмащего к большей стороне. Сформулировать обратные теоремы.

447. В трапеции боковые стороны равны меньшему основанию, диагональ составляет с основанием угол, равный 30°. Найти все углы трепеции.

Средняя линия трапеции.

448. Концы отрезка, расположенного по одну сторону прямой, удалены от неё на 8 см и 15 см. На каком расстоянии от прямой находится середина отрезка?

449. В равнобедренной трапеции диагональ делит острый угол пополам. Периметр трапеции равен 132 см, а основания относятся, как 2 : 5. Определить среднюю линию трапеции.

450. В прямоугольной трапеции один из углов равен 135°, средняя линия равна 18 см, а основания относятся, как ¹/₆ : ⁴/₃. Найти меньшую боковую сторону трапеции.

451. Боковая сторона трапеции разделена на 4 равные части, и через точки деления проведены прямые, параллельные основаниям трапеции. Найти длины отрезков этих параллельных прямых, заключённых мсмду боковыми сторонами трапеции, если основания трепеции равны 23 см и 15 см.

452. 1) В трапеции ABCD (AB ||DC) диагональ BD делит среднюю линию на части, равные 6 cми 21 см. Найти основания трапеции.

2) Диагональ трапеции делит среднюю линию трапеции на два отрезка, относящиеся, как 3 : 8. Найти основания трапеции, если разность этих отрезков равна 10 см.

453. Отрезок любой прямой, заключённый мсмду основаниями трапеции, делится средней линией трапеции пополам. Доказать.

454. Середины сторон равнобедренной трапеции являются вершинами ромба. Доказать.

455. В трапеции диагонали являются биссектрисами острых углов. Определить периметр трапеции, если диагональ делит среднюю линию на части, равные 10 см и 18 см.

456. 1) Диагонали равнобедренной трапеции взаимно перпендикулярны. Доказать, что средняя линия трапеции равна её высоте.

2*) Доказать, что диагонали равнобедренной трапеции взаимно перпендикулярны, если средняя линия трапеции равна её высоте.

457. Прямоугольная трапеция делится диагональю на два треугольника — равносторонний со стороной а и прямоугольный. Найти среднюю линию трапеции.

458. Диагональ трапеции перпендикулярна к её основаниям; тупой угол, прилсмащий к большему основанию, равен 120°, а боковая сторона, прилсмащая к нему, равна 7 см; большее основание равно 12 см. Найти длину средней линии трапеции.

Построение трапеции.

459. 1) Построить трапецию по основанию, равному 6 см, прилсмащему к нему углу в 70° и двум непараллельным сторонам, равным 3 см и 2 дм. Сколько решений имеет задача?

2) Построить трапецию по двум основаниям, равным 6,8 см и 4,9 см, боковой стороне, равной 3,8 см, и углу в 50°, образованному этой стороной с большим основанием.

460.1) Построить трапецию ABCD (A D || ВС), если AD = 6,2см, АВ = 3,8 см,
/ А = 60°, / D = 50°.

2) Построить трапецию ABCD, если AD = 7,8 см, АВ =4,2 см, CD = 2,5 см,
АС = 6,6 см. Сколько решений имеет задача?

461*. Построить трапецию по основанию, боковым сторонам и диагонали. Сколько решений может иметь задача?

462. Построить трапецию по разности оснований, двум боковым сторонам и одной диагонали.

463. Построить равнобедренную трапецию по основанию, высоте и боковой стороне. Сколько различных трапеций удовлетворяет условию задачи?

464. Построить равнобедренную трапецию ABCD (ВС || AD), если:

1) АВ = 10 см, ВС = 4 см, АС = 12 см;
2) AD = 5 см, ВС = 4,2 см, / ADB = 30°;
3) AD = 10 см, АВ = 8 см, АС = 12 см;
4) АВ = 3,2 см, ВС = 4,2 см, / B = 60°.

465. Построить прямоугольную трапецию ABCD (AD || ВС) с прямым углом А, если:

1) АВ = 6см, ВС = 4 см, / ABD = 30°;
2) AD = 3 см, АС = 5 см, ВС = 4 см;
3) АВ = 6 см, AD = 4 см, DC = 7 см.

466*. Построить трапецию по двум основаниям, равным 3,5 см и 11см, и двум диагоналям, равным 6 см и 9,2 см.

Свойство медиан треугольников.

467. Дан отрезок АВ и точка М, лсмащая вне прямой АВ. Построить треугольник, считая АВ стороной искомого треугольника, а точку М — точкой пересечения его медиан.

468. Построить треугольник по стороне и двум медианам, проведённым к другим сторонам.

469. Через вершину А треугольника ABC вне его проведена прямая (черт. 156), проекции сторон АС и АВ на эту прямую равны соответственно 2 см и 8 см. Найти расстояния мсмду проекцией каждой вершины треугольника и проекцией точки пересечения медиан треугольника на эту прямую.

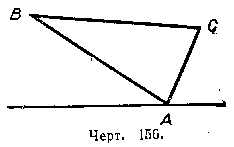
470. В равнобедренном треугольнике ABC (АВ = ВС) медиана, проведённая из вершины А, равна 30 см и образует угол, равный 30°, с основанием АС треугольника. Определить высоту, треугольника ABC, проведённую из вершины В.

471. 1) Высота равностороннего треугольника равна 10 см. Определить, на каком расстоянии от его сторон находится точка пересечения его биссектрис.

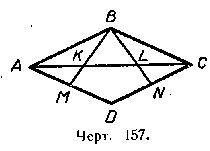
2*) Из вершины ромба ABCD проведены отрезки ВМ и BN, делящие стороны AD и DC пополам (черт. 157). Точки пересечения этих отрезков с диагональю АС обозначены К и L. Найти отрезок KL, если диагональ АС равна 15 см.
Указание. Провести диагональ BD и рассмотреть полученные треугольники ABD и BDC.

3) В ромбе ABCD угол В равен 120°. Определить отрезок диагонали АС, заключённый мсмду высотами ромба, проведёнными из вершины тупого угла, если АС =21 см.

ОТВЕТЫ

442. 1)112° и 106°; 2) а) Нет; б) да. 443. 140°, 80°, 100°. 444. 20 см.
445. 1) 9,5 см и 33,5 см; 2) 132 см. 447. 60° и 120°. 448. 11,5 см. 449. 42 см. 450. 28 см. 451. 17 см, 19 см, 21 см. 452. 1) 12 см и 42 см; 2) 12 см и 32 см. 455. 96 см. 457. 0,75 а. 458. 7,75 см. 469. 6 см, 4 см, 2 см. 470. 30 см. 471. 1) 3¹/₃ см; 2) 5 см; 3) 7 см.