ГЛАВА VII.

ОКРУЖНОСТЬ.

§ 22. Взаимное положение прямой и окружности,
взаимное положение двух окружностей.

Касательная к окружности.

634. Через точку, данную на дуге окружности, не определяя её центра, провести к окружности касательную.

635. Около круга радиуса 10 см описана равнобедренная трапеция с острым углом, равным 30°. Найти её боковую сторону.

636. Около круга радиуса R описан ромб. Найти его высоту.

637. Две окружности имеют общий центр. Доказать, что хорды большей окружности, касающиеся меньшей окружности, равны между собой.

638*. Провести касательную к данной окружности, параллельную данной прямой. Рассмотреть случаи, когда:
а) центр окружности находится вне чертежа;
б) центр окружности известен.

639. 1) К данной окружности провести две касательные, составляющие между собой данный угол.

2) К данной окружности провести касательную, составляющую с данной прямой данный угол α.

640. Данным радиусом описать окружность, которая касалась бы данной прямой в данной на ней точке.

641*. На практике часто для проведения касательной к данной окружности через данную вне её точку пользуются одной линейкой. Решить следующие задачи, используя указанный приём построения касательной:
а) построить треугольник по стороне и высотам, проведённым к двум другим сторонам;
б) построить треугольник по двум сторонам и высоте, проведённой к третьей стороне; в) построить равнобедренный треугольник по основанию и высоте, проведённой к боковой стороне.

642. Диаметр АВ и хорда АС окружности с центром в точке О образуют угол, равный 30°. Касательная, проходящая через точку С, пересекает прямую АВ в точке D. Доказать, что ОС = ¹/₂ОD.

643*. Через точку В, взятую на окружности, с центром вточке О, проведены хорда АВ (дуга АВ меньше 90°) и касательная к окружности. Продолжение диаметра, перпендикулярногорадиусу ОА, пересекает касательную и продолжение хорды соответственно в точках С и D. Доказать, что отрезки ВС и CD равны.

644. В данный угол вписать окружность радиуса 4 см.

645. 1) Доказать, что две касательные, проведённые к одной окружности через одну точку, взятую вне окружности, равны.

2) Касательные к окружности образуют угол, равный 60°. Доказать, что:
а) отрезок, соединяющий их точку пересечения с центром окружности, равен диаметру окружности;
б) отрезок, соединяющий точки касания, равен длине касательной от точки пересечения касательных до точки касания.

646. Угол ВАС, образованный касательными АВ и АС к одной окружности, равен 60°; длина ломаной линии ВАС равна 1 м. Определить расстояние между точками касания В и С.

647. Из точки, лежащей вне окружности радиуса R, проведены к ней две взаимно перпендикулярные касательные. Найти длину каждой касательной.

648. Доказать, что общие внутренние касательные АВ и CD к двум окружностям равны (A,B,C,D — точки касания, черт. 198).

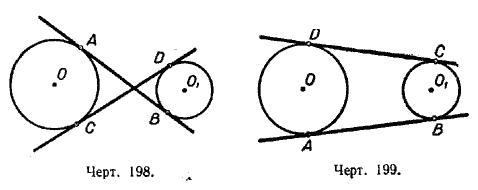
649. На чертеже 199 АВ и CD — общие внешние касательные к двум окружностям
(А, В, С и D — точки касания). Доказать, что АВ = CD.

650. Через точку М, взятую вне окружности, проведены к ней касательные МА и MB
(А и В — точки касания), и через произвольную точку С меньшей дуги АВ проведена касательная KL к окружности. Доказать, что периметр треугольника KML (черт. 200) не зависит от положения точки С.

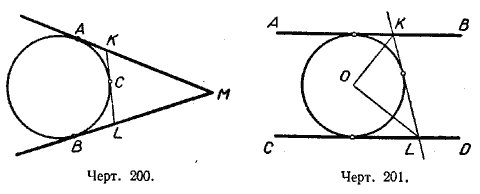
651. На чертеже 201 АВ, CD, KL — касательные к окружности, АВ параллельна CD. Доказать, что / KOL равен 90°.

Взаимное положение двух окружностей.

652. Как расположены друг относительно друга две окружности, если:
а) расстояние между их центрами равно 15 см, а радиусы их равны 3 см и 8 см;
б) расстояние между их центрами равно 200 мм, а диаметры их равны 320 мм и 80 мм; в) расстояние между их центрами равно 8 см, а диаметры их равны 20 см и 2 см;
г) расстояние между их центрами равно 200 мм, а радиусы их равны 420 мм и 260 мм?

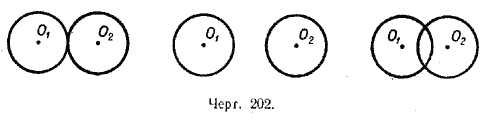
653. Начертить окружности, расположенные друг относительно друга так, как это указано на чертеже 202, построить центр симметрии и оси симметрии для каждого случая расположения окружностей (окружности имеют равные радиусы).

654. Найти радиусы двух окружностей, имеющих общий центр, если диаметр большей окружности делится меньшей окружностью на 3 части, равные 9 см, 12 см, 9 см.

655. 1) Радиусы двух окружностей, имеющих общий центр, относятся, как 2 : 7. Найти диаметры этих окружностей, если ширина кольца, образованного ими, равна 24 см.

2) Найти диаметры двух окружностей, имеющих общий центр, если известно, что они относятся, как 2 : 5, а одна из трёх частей, на которые диаметр большей окружности делится меньшей окружностью, равна 9 см (два решения).

656. 1) Две окружности касаются внешним образом. Радиусы окружностей относятся, как 2 : 3. Найти диаметры окружностей, если расстояние между центрами окружностей равно 10 см.

2) Две окружности касаются внутренним образом. Определить радиусы этих окружностей, если они относятся, как 5 : 2, а расстояние между центрами равно 15 см.

657. 1) Две окружности расположены одна внутри другой. Диаметр большей окружности, проходящий через центр меньшей окружности, делится меньшей окружностью на три части, равные 2 см, 10 см и 6 см. Найти диаметры окружностей и расстояние между центрами окружностей.

2) Две окружности, радиусы которых относятся, как 2 : 5, расположены одна внутри другой. Диаметр большей окружности, проходящий через центр меньшей окружности, делится меньшей окружностью на три части, крайние из которых равны 10 см и 5 см. Найти радиусы этих окружностей и расстояние между их центрами.

658. Общая хорда двух равных пересекающихся окружностей, радиус которых равен R, видна из их центров под углом 120°. Сделать чертёж. Найти расстояние между центрами окружностей.

ОТВЕТЫ