О РЕШЕНИИ ТРЕУГОЛЬНИКОВ.

X. Косоугольные треугольники.

§ 103. Формулы для определения углов треугольника по трем сторонам.

1)   Из равенства  а² = b² + с² — 2bс • соs A  находим:

,

но при многозначных числах эта формула неудобна.

2)  Следующие преобразования той же формулы приводят к выражениям, пригодным для логарифмирования:

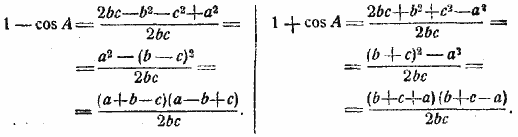
Заменяя первые части (по §60) и полагая а + b + с = 2p, получим далее:

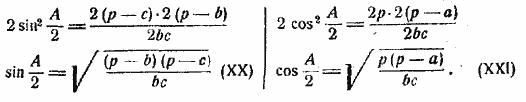
Так как в  треугольнике  половина, угла   всегда   менее 90°,  то sin  и cos  положительны,  что и принято во внимание при извлечении корня. Деля равенство (XX) на (XXI), найдем:

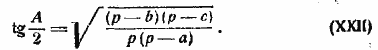
Формулы для определения углов В и С можно написать по аналогии с выведенными для угла А.

Формуле (XXII) можно придать другой вид, более удобный для  вычисления   в  том  случае,   когда  надо  вычислить все  три угла; а именно: умножая под корнем числитель и знаменатель на р — с, получим:

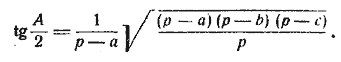
Подкоренное выражение здесь не зависит от того, какой угол определяется, а потому, обозначая величину корня через k, будем иметь:

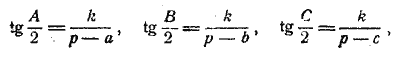
где

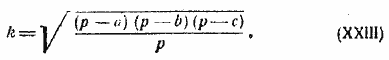
§ 104. Тангенс половины угла треугольника можно определить также с помощью радиуса   вписанного   круга.

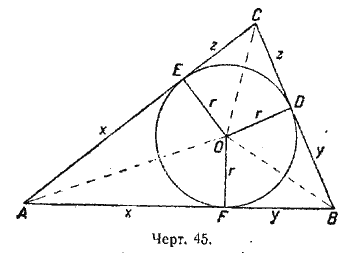
Пусть (черт. 45) будут: О —центр вписанного круга; D, Е и F—точки касания; r —длина радиуса. Заметим, что линии ОА, ОВ и ОС делят углы треугольника пополам и что отрезки сторон при общей вершине равны (например AE =AF). Сначала определим эти отрезки. Обозначая их в порядке вершин треугольника через х, у и z, получим:

x + y + z = р,   но у + z = ВC = а,

следовательно,   x  = p — а . Подобным же   образом у = р — b и z = p — c.  Теперь из  прямоугольных треугольников найдем:

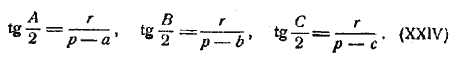
Чтобы произвести вычисление по этим формулам, надо сперва определить r (или только lg r); для этого послужат геометрические формулы:

_____________________________
 

откуда

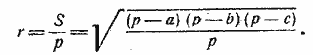
(Сравнивая последнее выражение с выражением  k в § 103, видим, что k = r.)

§ 105. О независимых соотношениях между сторонами и углами косоугольного треугольника. Этих соотношений должно быть т р и. Таковы соотношения:

A + B + C= 180°...                                (a)

^a/_{sin A}  = ^b/_{sin B} = ^c/_{sin C}  ^2)...                     (b),

_____________________
 ²⁾ Тут д в е независимых пропорции: ^a/_{sin A}  = ^b/_{sin B}   и  ^a/_{sin A}  = ^c/_{sin C}

Остальное можно вывести отсюда.

В §§100 и 101 образованы пропорции, производные от (b). В § 102 мы ссылались на геометрическую теорему. Теперь выведем то же самое из равенств (а) и (b).

Обозначая в равенстве (b) величину каждой части через m, будем иметь:

a = m • sin A;   b = m • sin B;   c =  m • sin C...                    (c)

Возьмем a = m • sin A.  Так как по (а) А+ (В+ С) = 180°, то sin A = sin(B + С); таким образом:  a = m •  sin (B + C) и, следозэтельно:

a² = m² •  sin² (B + C)...                                   (d)

Преобразуем:

sin² (B + C) = (sin В • cos С + cos В • sin C)² =
= sin² В (1 — sin²С) + (1 — sin² В) sin² С + 2 sin В • sin C • cos B • cos С =
= sin² В + sin² С +2 sin В • sin С (cos В • cos С — sin B • sin C) =
= sin²В + sin² С + 2 sin B • sin C • cos (B + C),

но cos (B + C) = — cos A; следовательно,

sin² (B+ C)= sin² В + sin² С — 2 sin B • sin C • cos A.

Подставляя это в равенство (d), получим:

a² = m² •  sin² B+  m² •  sin² C — 2 (m • sin В) (m • sin C ) • cos A .

или по равенству (с):

а² = b² + с² — 2bс • соs A.

.