О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ.

(ГОНИОМЕТРИЯ.)

III. Углы отрицательные. Углы, большие 360°.

§ 38. Общность формул приведения.

В §§ 17, 30 и 34 было показано, как приводятся к углу α тригонометрические функции следующих аргументов: — α; 90° ± α; 180° ± α; 270° ± α и 360° — α; при этом предполагалось, что угол α —положительный острый. Покажем теперь, что полученные формулы обладают общностью, т. е. что они верны и в том случае, если под α будем понимать какой угодно угол, от — ∞ до + ∞. Достаточно обнаружить это для синуса и косинуса, потому что остальное получится как следствие.

При доказательстве мы воспользуемся, между прочим, тем, что линия косинуса есть проекция подвижного радиуса на горизонтальный диаметр, а линия синуса равна его проекции на вертикальный диаметр.

Переходим к самому доказательству.

§ 39. 1. Пусть α означает какой угодно угол, тогда — α будет означать угол с такой же абсолютной величиной, но противоположный по знаку. Легко убедиться, что в таких углах подвижные радиусы лежат по разные стороны горизонтального диаметра в одинаковом отклонении от него; поэтому линии синуса у них равны, но направлены противоположно, а линии косинуса совпадают; отсюда заключаем, что
sin(— α) = —sin α и cos(—α) = cos α.

§ 40. 2. а) Представим 90° + α в виде α + 90°. Если к какому-нибудь углу прибавить 90°, то подвижной радиус перейдет в следующую четверть и составит с вертикальным диаметром такой же острый угол, какой раньше составлял с горизонтальным диаметром, и наоборот; поэтому его новая вертикальная проекция будет равна прежней горизонтальной, а новая горизонтальная проекция будет равна прежней вертикальной. Отсюда следует, что sin (α + 90°) и cos (α + 90°) имеют соответственно такую же абсолютную величину, как cos α и sin α. Что же касается знаков, то они будут таковы, в зависимости от четверти, где оканчивается угол α:

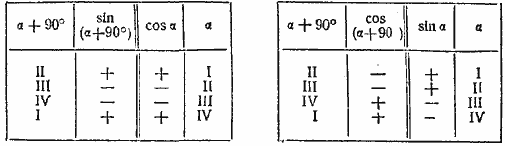
Видим, что sin (α + 90°) и cos α  имеют всегда одинаковые   знаки, а cos (α + 90°)  и
sin α — противоположные. Таким образом:

sin (90° + α) = cos α;
cos (90° + α) = sin α.

б) Применяя только что полученные формулы к углу — α и пользуясь § 39, найдем:

sin (90° — α) = cos (— α) = cos α;
соs (90° — α) = — sin (— α) = sin α.

§ 41. 3. а) Представим 180° + α в виде α +180°. Если к какому-нибудь углу прибавить 180°, то подвижной радиус перейдет в противоположную четверть и составит одну прямую со своим прежним положением (Или: конец дуги перейдет в точку, диаметрально противоположную.) следовательно, синус и косинус сохраняют свою абсолютную величину, а знаки обоих изменятся; поэтому:

sin (180° + α) = — sin α;
cos (180° + α) = — cos α.

б) Применяя эти формулы к углу — α, получим:

sin (180° — α) = — sin (— α) = sin α;
cos (180° — α) = — cos (— α) = — cos α.

§ 42. 4. а) Представим 270° + α  в виде α + 270°. Если к какому-нибудь углу прибавить 270°, то подвижной радиус изменит свое положение так же, как от поворота на — 90°. Рассуждая, как в § 40, заключим,   что вертикальная и горизонтальная проекции подвижного радиуса обменяются длиной, а потому абсолютные величины sin (α + 270°) и cos (α + 270°) соответственно равны абсолютным величинам cos α и sin α. Чтобы сравнить знаки, предположим конец α последовательно в каждой четверти:

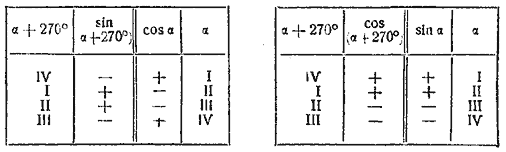
Видим, что sin (α + 270°) и cos α имеют всегда противоположные знаки, а
cos (α + 270°) и sin α одинаковые. Таким образом:

sin (270° + α) = — cos α;
cos (270° + α) = sin α.

б) Применяя эти формулы к углу — α, найдем:

sin (270° — α) = — cos (— α) = — cos α;
cos (270° — α) = sin (— α) = — sin α.

§ 43. 5. Представим 360° — α в виде — α + 360°. Если к какому-нибудь углу прибавить 360°, то окончательное положение подвижного радиуса не изменится; поэтому:

sin (360° — α) = sin (— α) = — sin α;
cos (360° — α) = cos (— α) = cos α.

§ 44. Формулы, полученные в §§ 39—43, имеют такой же точно состав, как и те, которые содержатся в §§ 17, 30, 34. Таким образом общность формул приведения доказана.

В задачах, — если требуется только припомнить формулу, — надо представить себе величину α между 0 и 90° и применить правило, данное в § 30.