О РЕШЕНИИ ТРЕУГОЛЬНИКОВ.

IX. Прямоугольные треугольники.

§ 83. Соотношения между элементами прямоугольного треугольника.

В § 20 были выведены тригонометрические соотношения между элементами прямоугольного треугольника; а именно, из  определения  тригонометрических  функций  были  выведены формулы (черт. 40):

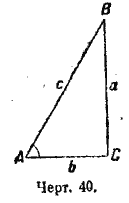
sin A = ^a/_c;    cos A = ^b/_c;    tg A = ^a/_b 

Определяя из этих формул а, b и с, найдем:

1) а = с • sin A  2) b = с • cos A;    3} а = b • tg A.

Словесные формулировки приведены в §§20—21. К  этим  формулам надо добавить еще три, известные из геометрии:

A + B = 90°;   c² = a² + b²;    S = ¹/₂ ab.

§ 84. Между элементами всякого треугольника существуют только три независимых соотношения. В состав треугольника входят три стороны и три угла; но из этих шести элементов достаточно иметь три (исключай случай трех углов), чтобы можно было построить треугольник и тем самым получить остальные три элемента. Отсюда следует, что и при вычислении в треугольнике можно определить три элемента по данным остальным; а для этого число различных уравнений между элементами треугольника должно быть равно также трем. Если уравнений получено более трех, то некоторые из них будут уже следствием других.

В прямоугольном  треугольнике основными соотношениями считаются обыкновенно следующие:

A + В = 90°;   а = с • sin A;   b = с • cos A.

Остальные можно вывести из них.

§ 85. Решение прямоугольных треугольников.

Основными элементами треугольника считаются стороны и углы. Поэтому при решении прямоугольного треугольника в зависимости от того, какие элементы даны, могут представиться 4 случая, разобранные в следующих параграфах. При этом в числе данных непременно должен быть один линейный элемент, так как иначе нельзя узнать размеры треугольника: по трем углам можно построить сколько угодно подобных треугольников.

Решение треугольников (как и решение всяких математических задач) проводится сначала, по возможности, до конца в общем виде; затем подставляются числовые данные и производятся вычисления. Все нижеследующие примеры решены с помощью таблиц Брадиса, сначала по натуральным значениям тригонометрических функций, потом — по логарифмам.

На случай пользования пятизначными таблицами сохранены примеры решения треугольников и по этим таблицам.

§ 86. 1-й  случай.   Даны   гипотенуза и острый   угол (с и А). Найти другой острый угол, катеты и площадь (В, a, b, S).

I.  Решение в общем виде.

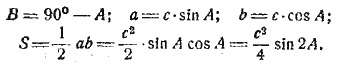
II.  Числовой пример: с = 627; A = 23°30'

Решение.

В = 90° — 23°30' = 66°30';    а = 627 • sin 23°30'

По таблице  VIII  Брадиса   находим   sin 23°30' = 0,3987; следовательно :

 а = 627 • 0,3987 = 249,9849;
 а ≈ 250 (лин. единиц);
 b = 627 • cos 23°30' = 627 • 0,9171 = 575,0227.
 b ≈ 575 (лин. единиц);
 S = ¹/₂  • 249,98 • 575,02 = 71 872 (кв. единиц). л

§ 87. 2-й случай.  Даны  катет и  острый угол (а и А). Найти В, с, b, S.

I.  Решение  в  общем   виде.

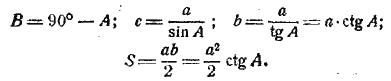
II.  Числовой  пример: а =18; А = 47°.

Решение.

§ 88.  3-й  случай.  Даны   гипотенуза  и  катет (с и а).  Найти А, В, b, S.

I.  Решение  в  общем   виде.

sin A = ^a/_c;    cos B = ^a/_c;   b = √c²— a² ;   S = ^a/₂ √c²— a² .

II.  Числовой пример: с = 65; а =16.

I    Решение.

sin A= ¹⁶/₆₅ = 0,2461;    А = 14°12' + 3' = 14°15';
В = 90° — 14°15' = 75°45';

b = √65² —16²  = √(65 + 16) (65 —16) = √81 • 49 = 9 • 7;
b = 63 (лин. единиц);

S = ¹⁶/₂ • 63 = 504 (кв. единиц).

§ 89. 4-й  случай.  Даны оба катета (а и b). Найти А, В, с, S.

I. Решение в общем виде.

 tg A = ^a/_b ;  tg B = ^b/_a ; c = √a²+ b² ; S = ^ab/₂

II. Числовой пример: a = 25; b =  40.

Решение.

tg A = ²⁵/₄₀ = 0,625;    A = 32°;    B = 58°;
c = √25² +40²  ≈  47,2;   S = 500 (кв. единиц).