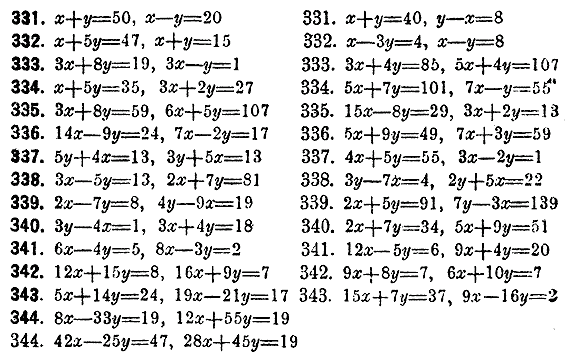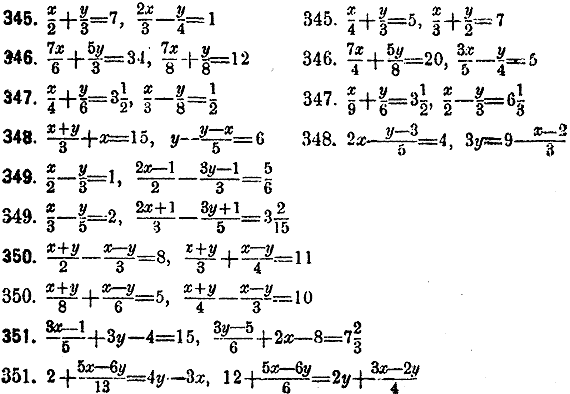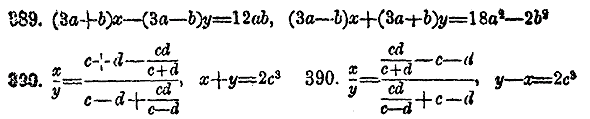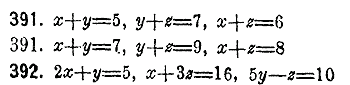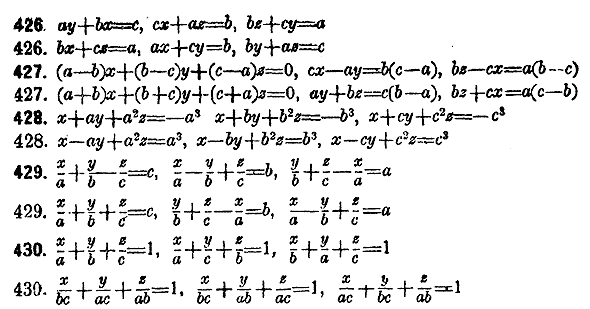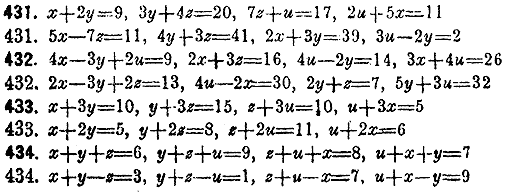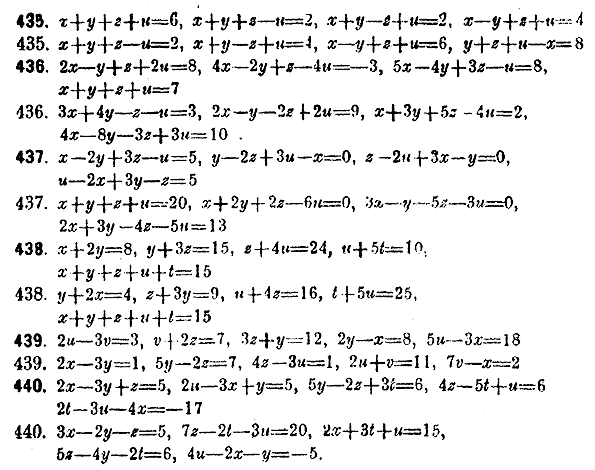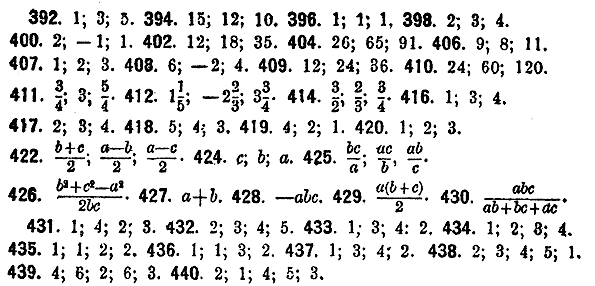|
ОТДЕЛЕНИЕ VI. ПРЕОБРАЗОВАНИЯ РАВЕНСТВ. ___________ РЕШЕНИЕ И СОСТАВЛЕНИЕ УРАВНЕНИЙ 1-Й СТЕПЕНИ § 6. Рeшение системы уравнений. Уравнениe первой степени с двумя неизвeстными может быть преобразовано посрeдством уничтожения знамeнателой входящих в него дробей, перенесения членов и соединeния их в группы к виду уравнения ах+bу=с, т.е. такому, в котором всe члены, содержащие то или другое неизвeстное, соединены в двух группах в первой части уравнения, а извeстный член находится во второй части и при этом а, b и с суть цeлыя количества, положительные или отрицательные. Предыдущеe уравнение называeтся общим видом уравнения первой степени с двумя неизвeстными. Количества а, b и с называютея коэффициентами уравнения. Пусть, напр., дано уравнение Для отыскания опредeленных значений двух неизвeстных необходимо и достаточно имeть два различных и совмeстных уравнения первой степени с этими неизвeстными. Что это необходимо, видно из того, что при одном данном уравнении каждое неизвeстное может имeть любое значение, лишь бы значение другого было подобрано соотвeтственно первому. Напр., если хотим, чтобы в уравнении 3х—2у=32 неизвeстноe х равнялось 5, то таким его и примем, а затeм, подставив это значение в уравнение, получим новое уравнение 15—2у=32, которое даст у= —81/2, и это есть значсние у-ка, соотвeтствующев значению х-са, равному 5. Точно также, если хотим считать у равным 5, то, замeнив его этим значением, находим уравнение 3х—10=32, которое дает соотвeтствующее значение у =14. Что совокупность двух уравнений достаточна для рeшения их по двум неизвeстным, видно из того, что существуют способы, посредством которых два уравнения могут быть рeшены. Рeшeние двух уравнений с двумя неизвeстными состоит главным образом в том, что данная пара уравнений замeняeтся другой парой, в состав которой входит одно из данных уравнений и новоe, третьe уравнение, содержащее одно только из прeжних неизвeстных. Имeя такую пару, можно из того уравнения, в которое входит одно неизвeстное, найти это неизвeстноe, а затeм, подставив найденноe значениe в другоe уравнeниe, опрeдeлим и другое неизвeстноe. Из этого видно, что при рeшeнии двух уравнeний с двумя неизвeстными главноe вычисление состоит в нахождении уравнения, совмeстного с данными и содержащего одно нeизвeстное. Такоe вычислениe называется исключeниeм неизвeстного. Оно производится разными способами, из которых важнeйшиe суть способ уравнивания коэффициентов и способ подстановления. Первый способ заключается в примeнении слeдующего правила: Для исключения одного нeизвeстного из двух уравнений первой степени с двумя неизвeстными, нужно составить наименьшее кратное коэффициентов исключаемого неизвeстного. Помножив обe части каждого из уравнений на дополнитeльный множитель к содержащемуся в уравнeнии коэффициeнту этого неизвeстного и, уравняв таким образом коэффициенты, сложить уравнения или вычесть, смотря потому, имeют ли уравненныe коэффициенты различныe знаки или одинаковые. Напр., если даны уравнения 3х—2у=32 и 5х +3у= —10, то замeчаем, что наименьшeе кратноe коэффициeнтов у-ка есть 6; умножая первое уравнениe на 3 и второe на 2, получим уравнения 9х— 6у = 96 и 10х + 6у = —20; наконeц, складывая послeдние уравнeния, находим 19х =76, что и представляет искомый рeзультат исключeния. Второй способ опрeдeляeтся таким правилом: Для исключения неизвeстного из двух уравнений с двумя неизвeстными нужно выразить исключаемое неизвeстноe чeрез другое при посрeдствe одного из данных уравнений и полученное выражение подставить в другоe уравнениe. Напр., имeя уравнeния 3х—2у=32 и 5х +3у= —10, выражаем из первого у в видe В дополнениe к вышесказанному замeтим еще, что для рeшeния двух уравнений с двумя неизвeстными необходимо, чтобы данныя уравнения были различны между собой и в то же врсмя совмeстны, т.е. с одной стороны нe вытeкали бы одно из другого, как слeдствие, и с другой стороны не противорeчили бы одно другому. Так, напр., два уравнения 9х— 6у=96 и 6х—4у=64 нe годятся для опредeленного рeшения, потому что оба они приводятея к уравнению 3х—2у=32 и одно из них выводится из другого. Подобно этому уравнения 6х—4у=64 и 15х—10у=70 не могут быть рeшены в обыкновенном смыслe слова, потому что они приводятся к уравнениям
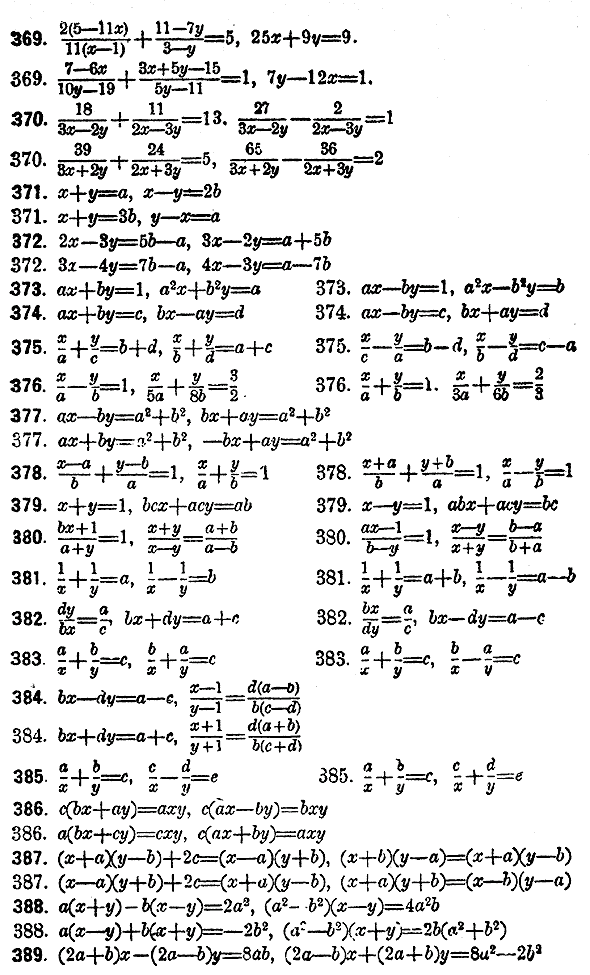
Общий вид уравнения с тремя неизвестными есть ах + bу + сz = d, где а, b, с и d суть целыя количества или буквенныe выражения. Для определения трех неизвестных необходимо и достаточно иметь три различные и совместные уравнения. Решение системы трех уравнений с тремя неизвестными состоит в том, что данную систему заменяют другой, в которой одно уравнение содержит три не-известных, другое содержит два неизвестных и третье только одно неизвестное, Для этого из всех трех уравнений данной системы исключают одно неизвестное и получают систему двух уравнений с двумя неизвестными. Исключив в этой системе одно неизвестное, получают одно уравнение с одним неизвеетным. Исключение неизвестных производится теми же способами, которые были разъяснены выше. ІІоложим, напр., что дана система уравнений 2х— 3у + 5z = 27, 3х + 6у— 4z =2, 5x + 4y + 2z =40. Решим ее по споcобу уравнивания коэффициентов. Исключим неизвестное z из всех трех уравнений. Для этого берем сначала первое уравнение вместе с третьим, помножим обе части первого на 2, что даст 4х— 6у + 10z=54, обе части третьего на 5, отчего получится 25x + 20y + 10z=200, затем вычитаем первый результат из последнего. Получаем уравнение с двумя неизвестными 21x + 26y =146. После этого берем второе уравнение вместе с третьим. При этой комбинации нужно только обе части третьего уравнения умножить на 2 и сложить полученное уравнение со вторым. Получим второе уравнение с двумя неизвестными 13x+14у=82. Исключая неизвестное у из полученных двух уравнений, находим уравнение с одним неизвестным 22x=44. Таким образом, мы имеем теперь, во-первых, три данных уравнения, каждое с тремя неизвестными, затем два производних уравнения, каждое с двумя неизвестными и, наконец, одно производное уравнение с одним неизвестным. Взяв одно из данных уравнений с тремя неизвестными, напр., первое, одно из провзводных с двумя неизвестными, напр., второе, и наконец последнее уравнение с одним неизвестным, составим систему трех уравнений 2х— 3у + 5z = 27, 13x+14у=82, 22x=44, которая совместна с данной и легко решается, потому что из последнего уравнения находвим x=2, затем, подставив это вначение х во второе уравнение, получим у=4 и, наконец, подставив значения х и у в первое уравнение, определим z =7. Предыдущая система трех уравинений называется разрешающей системой для отличия ее от данной, из которой она вытекает, как следствие. Решим ту же данную систему по способу подстановления. Исключим опять сначала неизвестное z. Для этого, пользуясь одним из данных уравнений, напр., третьим, выразим z через х и у в виде ІІолучим Таким образом найдено одно неизвестное. Подставляя значение х в выражение у, находим В этом случае, разрешающая система составляется тремя уравнениями x=2, Объяснения, данные в предыдущем примере, показывают, как можно решить систему трех уравнений в наиболее общем случае, когда эти уравнения не представляют никаких особенностей. В частных же случаях этот прием решения может допускат значительные упрощения. В особенности упрощается решение сисстемы тогда, когда одно или несколько из ее уравнений суть так называемые неполные, т.е. содержат только два из неизвест-ных, или даже одно. В следующих примерах учащиеся встретятся с образцами разнообразных упрощений.
Рeшeние системы уравнений со многими неизвeстными выполняeтся тем же способом послeдовательного исключения неизвeстных, который уже разъяснен вышe. Для возможности рeшения необходимо имeть столько различных уравнений, сколько есть неизвeстных. Когда такая систсма дана, то сначала из всeх ее уравнений исключают одно какое-нибудь неизвeстиоe, отчего получается новая система, содержащая одним уравнением меньше, чeм данная. Из всeх уравнений полученной системы опять исключают одно неиз-вeстное и таким образом составляют еще иную систему, которая содержит одним уравнением и одним неизвeстным меньше, чeм предыдущая. Так поступают до тeх пор, пока составится одно уравнение с одним неизвeстным. Послe этого, выбрав по одному уравнению от каждой систсмы, составляют из этих выбранных уравнений разрeшающую систему, в которой окажется одно уравнение с одним неизвeстным, одно с двумя, одно с тремя и т. д.. Вышеописанный общий план относится к наиболeе сложному случаю, когда всe данные уравнения и получаемые из них новые уравнения суть полные. В частных же случаях являются разнообразные упрощения, вслeдствие которых число составляемых уравнений иногда значительно уменьшается.
|
. Умиожив обe части его на 12, получим новое уравнение 96—(3х—2у)=6х—4у, котороe по раскрытии скобок примет форму 96— 3х+2у =6х—4у. Перенeся затем неизвeстные члены во вторую часть, найдем опять новое уравнение 96= 6х—4у+3х—2у,
которое послe приведения подобных членов примет форму 96=9х—6у или, переставляя части, форму 9х—6у=96. Это уравнеиие уже соотвeтствуст указанному общему виду, но обe части его можно ещe сократить на 3. Сдeлав это сокращение, получим опять новое уравнение 3х—2у=32,
котороe и есть окончательное. Из коэффициентов его второй отрицателен, вслeдствие чего для сравнения с общим видом полученное уравнeние слeдует писать в формe 3х+(—2)у=32.
и подставляeм это выражeние во второе уравнение, отчего получим уравнение с одним неизвeстным 
, приводящeеся к прежнeму 19х =76.
и полученное выражение вставим на место z в уравнения первое и второе. 
и 3х+6у—2(40—5х—4у)=2, или, по упрощении, 21x + 26y =146 и 1 3x+14у=82. Во втором из этих двух уравнений выражаем у через х в виде 
и полученное выражение вставляем на место у в первое
уравнение, которое вследствие этого примет вид 
или
и, наконец, вставляя значения х и у в выражение z, получим 
.
