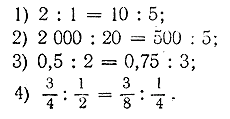|
Часть четвёртая. ПРОПОРЦИИ И ПРОПОРЦИОНАЛЬНОСТЬ ВЕЛИЧИН Глава девятнадцатая. Пропорции. § 125. Понятие о пропорции. Пропорцией называется равенство двух отношений. Вот примеры равенств, называемых пропорциями:
Примечание. Наименования величин в пропорциях не указаны. Пропорции принято читать следующим образом: 2 так относится к 1 (единице), как 10 относится к 5 (первая пропорция). Можно читать иначе, например: 2 во столько раз больше 1, во сколько раз 10 больше 5. Третью пропорцию можно прочесть так: - 0,5 во столько раз меньше 2, во сколько раз 0,75 меньше 3. Числа, входящие в пропорцию, называются членами пропорции. Значит, пропорция состоит из четырёх членов. Первый и последний члены, т. е. члены, стоящие по краям, называются крайними, а члены пропорции, находящиеся в середине, называются средними членами. Значит, в первой пропорции числа 2 и 5 будут крайними членами, а числа 1 и 10 — средними членами пропорции. § 126. Основное свойство пропорции. Рассмотрим пропорцию: 6 : 3 = 8 : 4. Перемножим отдельно её крайние и средние члены. Произведение крайних 6 • 4 = 24, произведение средних 3 • 8 = 24. Рассмотрим другую пропорцию: 10 : 5 = 12 : 6. Перемножим и здесь отдельно крайние и средние члены. Произведение крайних 10 • 6 = 60, произведение средних 5 • 12 = 60. Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних её членов. В общем виде основное свойство пропорции Проверим его на нескольких пропорциях: 1) 12 : 4 = 30 : 10. Пропорция эта верна, так как равны отношения, из которых она составлена. Вместе с тем, взяв произведение крайних членов пропорции (12 • 10) и произведение средних её членов (4 • 30), мы увидим, что они равны между собой, т. е. 12 • 10 = 4 • 30. 2) 1/2 : 1/48= 20 : 5/6 Пропорция верна, в чём легко убедиться, упростив первое и второе отношения. Основное свойство пропорции примет вид: 1/2 • 5/6 = 1/48 • 20 Нетрудно убедиться в том, что если мы напишем такое равенство, у которого в левой части стоит произведение двух каких-нибудь чисел, а в правой части произведение двух других чисел, то из этих четырёх чисел можно составить пропорцию. Пусть у нас имеется равенство, в которое входят четыре числа, попарно перемноженные: 10 •7 = 2 •35, эти четыре числа могут быть членами пропорции, которую нетрудно написать, если принять первое произведение за произведение крайних членов, а второе — за произведение средних. Изданного равенства можно составить, например, такую пропорцию: 10 : 2 = 35 : 7. Вообще, из равенства ad = bc можно получить следующие пропорции:
Проделайте самостоятельно следующее упражнение. Имея произведение двух пар чисел, напишите пропорцию, соответствующую каждому равенству: а) 1 • 6 = 2 • 3; б) 2 • 15 = б • 5. § 127. Вычисление неизвестных членов пропорции. Основное свойство пропорции позволяет вычислить любой из членов пропорции, если он неизвестен. Возьмём пропорцию: х : 4 = 15 : 3. В этой пропорции неизвестен один крайний член. Мы знаем, что во всякой пропорции произведение крайних членов равно произведению средних членов. На этом основании мы можем написать: x • 3 = 4 • 15. После умножения 4 на 15 мы можем переписать это равенство так: х • 3 = 60. Рассмотрим это равенство. В нём первый сомножитель неизвестен, второй сомножитель известен и произведение известно. Мы знаем, что для нахождения неизвестного сомножителя достаточно произведение разделить на другой (известный) сомножитель. Тогда получится: х = 60 : 3, или х = 20. Проверим найденный результат подстановкой числа 20 вместо х в данную пропорцию: 20 : 4=15 : 3. Пропорция верна. Подумаем, какие действия нам пришлось выполнить для вычисления неизвестного крайнего члена пропорции. Из четырёх членов пропорции нам был неизвестен только один крайний; два средних и второй крайний были известны. Для нахождения крайнего члена пропорции мы сначала перемножили средние члены (4 и 15), а затем найденное произведение разделили на известный крайний член. Сейчас мы покажем, что действия не изменились бы, если бы искомый крайний член пропорции стоял не на первом месте, а на последнем. Возьмём пропорцию: 70 : 10 = 21 : х. Запишем основное свойство пропорции: 70 • х = 10 • 21. Перемножив числа 10 и 21, перепишем равенство в таком виде: 70 • х = 210. Здесь неизвестен один сомножитель, для его вычисления достаточно произведение (210) разделить на другой сомножитель (70), х = 210 : 70; х = 3. Таким образом, мы можем сказать, что каждый крайний член пропорции равен произведению средних, делённому на другой крайний. Перейдём теперь к вычислению неизвестного среднего члена. Возьмём пропорцию: 30 : х = 27 : 9. Напишем основное свойство пропорции: 30 • 9 = х • 27. Вычислим произведение 30 на 9 и переставим части последнего равенства: х • 27 = 270. Найдём неизвестный сомножитель: х = 270 : 27, или х = 10. Проверим подстановкой: 30 : 10 = 27 : 9. Пропорция верна. Возьмём ещё одну пропорцию: 12 : б = х : 8. Напишем основное свойство пропорции: 12 . 8 = 6 • х. Перемножая 12 и 8 и переставляя части равенства, получим: 6 • х = 96. Находим неизвестный сомножитель: х = 96 : 6, или х = 16. Таким образом, каждый средний член пропорции равен произведению крайних, делённому на другой средний. Найдите неизвестные члены следующих пропорций: 1) а : 3= 10:5; 3) 2 :1/2 = x : 5; 2) 8 : b = 16 : 4; 4) 4 : 1/3 = 24 : х. Два последних правила в общем виде можно записать так: 1) Если пропорция имеет вид: х : а = b : с, то
2) Если пропорция имеет вид: а : х = b : с, то
§ 128. Упрощение пропорции и перестановка её членов. В настоящем параграфе мы выведем правила, позволяющие упрощать пропорцию в том случае, когда в неё входят большие числа или дробные члены. K числу преобразований, не нарушающих пропорцию, относятся следующие: 1. Одновременное увеличение или уменьшение обоих членов любого отношения в одинаковое число раз. П р и м е р. 40 : 10 = 60 : 15. Увеличив в 3 раза оба члена первого отношения, получим: 120:30 = 60: 15. Пропорция не нарушилась. Уменьшив в 5 раз оба члена второго отношения, получим: 40:10 = 12:3. Получили опять правильную пропорцию. 2. Одновременное увеличение или уменьшение обоих предыдущих или обоих последующих членов в одинаковое число раз. Пример. 16:8 = 40:20. Увеличим в 2 раза предыдущие члены обоих отношений: 32:8 = 80:20. Получили правильную пропорцию. Уменьшим в 4 раза последующие члены обоих отношений: 16:2 = 40:5. Пропорция не нарушилась. Два полученных вывода можно кратко высказать так: Пропорция не нарушится, если мы одновременно увеличим или уменьшим в одинаковое число раз любой крайний член пропорции и любой средний. Например, уменьшив в 4 раза 1-й крайний и 2-й средний члены пропорции 16:8 = 40:20, получим: 4:8 =10:20. 3. Одновременное увеличение или уменьшение всех членов пропорции в одинаковое число раз. Пример. 36:12 = 60:20. Увеличим все четыре числа в 2 раза: 72:24 = 120:40. Пропорция не нарушилась. Уменьшим все четыре числа в 4 раза: 9:3 = 15 : 5. Пропорция верна. Перечисленные преобразования дают возможность, во-первых, упрощать пропорции, а во-вторых, освобождать их от дробных членов. Приведём примеры. 1) Пусть имеется пропорция: 200 : 25 = 56 : x. В ней членами первого отношения являются сравнительно большие числа, и если бы мы пожелали найти значение х, то нам пришлось бы выполнять вычисления над этими числами; но мы знаем, что пропорция не нарушится, если оба члена отношения разделить на одно и то же число. Разделим каждый из них на 25. Пропорция примет вид: 8 :1 = 56 : x. Мы получили, таким образом, более удобную пропорцию, из которой х можно найти в уме:
2) Возьмём пропорцию: 2 : 1/2 = 20 : 5. В этой пропорции есть дробный член (1/2), от которого можно освободиться. Для этого придётся умножить этот член, например, на 2. Но о д и н средний член пропорции мы не имеем права увеличивать; нужно вместе с ним увеличить какой-нибудь из крайних членов; тогда пропорция не нарушится (на основании первых двух пунктов). Увеличим первый из крайних членов (2 • 2) : (2 • 1/2) = 20 : 5, или 4 : 1 = 20:5. Увеличим второй крайний член: 2 : (2 • 1/2) = 20 : (2 • 5), или 2 : 1 = 20 : 10. Рассмотрим ещё три примера на освобождение пропорции от дробных членов. Пример 1. 1/4 : 3/8 = 20:30. Приведём дроби к общему знаменателю: 2/8 : 3/8 = 20 : 30. Умножив на 8 оба члена первого отношения, получим: 2 : 3 = 20 : 30. Пример 2. 12 : 15/14= 16 : 10/7. Приведём дроби к общему знаменателю: 12 : 15/14= 16 : 20/14 Умножим оба последующих члена на 14, получим: 12:15 = 16:20. Пример 3. 1/2 : 1/48 = 20 : 5/6. Умножим все члены пропорции на 48: 24 : 1 = 960 : 40. При решении задач, в которых встречаются какие-нибудь пропорции, часто приходится для разных целей переставлять члены пропорции. Рассмотрим, какие перестановки являются законными, т. е. не нарушающими пропорции. Возьмём пропорцию: 3 : 5 = 12 : 20. (1) Переставив в ней крайние члены, получим: 20 : 5 = 12:3. (2) Переставим теперь средние члены: 3 :12 = 5 : 20. (3) Переставим одновременно и крайние, и средние члены: 20 : 12 = 5 : 3. (4) Все эти пропорции верны. Теперь поставим первое отношение на место второго, а второе — на место первого. Получится пропорция: 12 : 20 = 3 : 5. (5) В этой пропорции мы сделаем те же перестановки, какие делали раньше, т. е. переставим сначала крайние члены, затем средние и, наконец, одновременно и крайние, и средние. Получатся ещё три пропорции, которые тоже будут справедливыми: 5 : 20 = 3 : 12. (6) 12 : 3 = 20 : 5. (7) 5 : 3 = 20 : 12. (8) Итак, из одной данной пропорции путём перестановки можно получить ещё 7 пропорций, что вместе с данной составляет 8 пропорций. Особенно легко обнаруживается справедливость всех этих пропорций при буквенной записи. Полученные выше 8 пропорций принимают вид: а : b = с : d; c : d = a : b ; d : b = с : a; b : d = a : c; a : c = b : d; c: a = d : b; d : c = b : a; b : a = d : c. Легко видеть, что в каждой из этих пропорций основное свойство принимает вид: ad = bc. Таким образом, указанные перестановки не нарушают справедливости пропорции и ими можно пользоваться в случае надобности. |