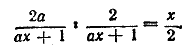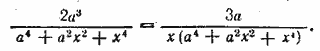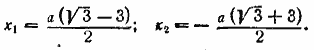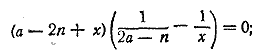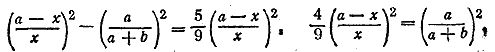ГЛАВА   3

АЛГЕБРАИЧЕСКИЕ    УРАВНЕНИЯ

При решении задач этой главы не рассматриваются исключительные значения известных величин, при которых данное уравнение теряет смысл или лишается решений, или приобретает больше решений. Так, в задаче 375 данное уравнение теряет смысл при b = 0 и при b—а =0, ибо при b = 0 знаменатели первого и второго членов обращаются в нуль, а при b—а = 0 то же происходит с последним членом.

Далее, при а = 0 данное уравнение имеет бесчисленное множество решений, так как уравнение принимает вид 1 = 1 и становится тождеством. Наконец, при b=3а данное уравнение совсем не имеет решений, так как оно приводится к виду 0 • у =7/18•

Ответы и решения

375.

Дробь представим    в    виде    Тогда   данное уравнение примет вид

откуда

Ответ

__________________________________________________

376.

Освобождаемся от знаменателя  (общий знаменатель а2 — b2).

Ответ x = 0.

__________________________________________________

377.

Решая данное уравнение по общему способу, получим

Эту дробь можно сократить, разложив числитель на множители (выражение 3abc представим в виде трехчлена abc+abc+abc и каждый из последующих членов сгруппируем с abc). Получим х = а+b+с.

Решение    упрощается с помощью    следующего    искусственного приема.

Слагаемое  представим в видеи аналогично два других слагаемых левой части. Уравнение примет вид:  

Ответ  x = a+b+c.

__________________________________________________

378.

 Общий знаменатель 6cd (2c+3d) (2с — 3d)

Ответ  

__________________________________________________

379.

Представим дробь в виде  (чтобы получить тот же знаменатель, что у следующей дроби). Дробь полезно преобразовать к видуПереносим все члены влево и группируем их (первый с четвертым, второй с третьим). Получаем

Преобразовав  к   виду, освободимся  от знаменателя.

Ответ    x = 3/4

__________________________________________________

380.

Переносим члены с x в левую часть уравнения, а известные в правую, и каждую часть отдельно приводим к общему знач менателю; получим

или

Отсюда

После сокращения находим

Ответ   

__________________________________________________

381.

 Производим группировку  членов, как  в задаче  140; после преобразований получим

Ответ

__________________________________________________

382.

Общий знаменатель (a+b)2 (a—b),

Ответ   

__________________________________________________

383.

  Дробь  представим   в   виде     Общий знаменатель будет     mz(z2—m2). Освободившись от него, получаем после приведения подобных членов     m2z 2— 4m3z = 0. Это уравнение имеет два корня: z = 0 и z = 4m . Но при отбрасывании знаменателя, содержащего неизвестную величину, могут появиться лишние корни; а именно, лишними будут те, которые обращают общий знаменатель в нуль. В данном случае лишним является корень z = 0. Он не удовлетворяет данному уравнению потому, что первый и третий члены теряют смысл при z =0. Корень z = 4m не обращает в нуль общий знаменатель; поэтому он не является лишним.

Ответ z = 4m

__________________________________________________

384.

Общий   знаменатель будет b4 — х2.   Освобождаясь   от   него, получим
2х(a2+b2— 2аb)=2 (а2 — b2),   откуда      Лишних корней нет,  потому что знаменатель  b4 — х2  не  обращается в нуль при .

Ответ

__________________________________________________

385.

Общий знаменатель (х2 — а2)(х + п). Освобождаясь от знаменателя, найдем  .При этом значении х знаменатель не обращается   в  нуль.   Значит,     есть  корень   данного  уравнения.

Ответ  

__________________________________________________

386.

Представим х + а—1 в  виде  х + 1/а     После  преобразовавний получим

Сокращая на ах + l , найдем х =2а.

Замечание. Сокращение на ах + 1 возможно при условии, что ах + 1 не равно нулю. Но при х =2а имеем ах + 1 = 2а2+1 >0. Поэтому полученный  корень — не лишний.   Но  если   бы мы  имели, например,   уравнение,то   сокращение   на    х — 2а дало бы  тоже х =2а.  Однако  этот  корень не  годится,   ибо дроби

теряют  смысл при х—2а. Таким   образом,   уравнение  не имеет решений:

Ответ х =2а

__________________________________________________

387.

Перепишем уравнение в виде

Общий  знаменатель левой  части     (a2+x2+ax) (а2+х2—ах)     можно преобразовать так:

(а2+х2)2— (ах)2 = а4+а2х2+х4.

Получаем

Ответ  

__________________________________________________

388.

Переносим члены  с неизвестным  в  левую  часть уравнения, а члены, не содержащие неизвестного, в правую:

(а— b—1)√x  = (а2 — b2) — (а + b ).

После разложения правой части на множители получим

(а— b—1)√x  =(а + b )(а— b—1).

Отсюда имеем  √x = а + b.

Так как  выражение √x означает  положительное значение   квадратного корня, то при   а + b < 0 задача не имеет решения.

Ответ х = (а + b )2 (при условии, если а + b>0).

__________________________________________________

389.

После освобождения   от знаменателя и  приведения   подобных членов получим
2х2 +6ах+3а2 =0.

Ответ

__________________________________________________

390.

Общий   знаменатель будет 4(x+b) (x—b).  После    упрощения получим

12х2—4bx—b2=0.

Ответ x1 = b/2   ;  x2= — b/6

__________________________________________________

391.

Общий знаменатель будет  (х—а)2. После освобождения от знаменателя получим

 (х—а)2—2а  (х—а) + (а2—b2) =0.

Из этого квадратного уравнения находим

х — а = а±b.

Ответ x1= 2а+b   x2= 2а—b

__________________________________________________

392.

Общий знаменатель будет bc2 (a—2b). После освобождения от знаменателя получим

(сх)2—(a—2b) •(сх) — b(a—b)=0.

Из этого уравнения находим

Ответ

__________________________________________________

393.

  Освобождаясь     от      знаменателя,      получим      уравнение 4х (х—а)+8х (х+а) =5а2 или, после упрощения,

12х2+4ах—5а2 = 0.

Ответ

__________________________________________________

394.

Общий   знаменатель  п (пх—2).   После   упрощений   уравнение принимает вид

(п — 1)х2—2х— (п +1)=0.

Ответ

__________________________________________________

395.

Общий знаменатель будет а (а—х)2. После  упрощений   получим уравнение

(а +1) х2—2ах + (а —1) = 0.

Ответ

__________________________________________________

396.

Общий знаменатель будет (х—а)2. После освобождения от знаменателя получаем уравнение

(х—а)2—2b (х—а) — (а2—b2) = 0,

решая которое, находим

х— а = b ± а.

Ответ x1 = 2a + b ;   x2= b

__________________________________________________

397.

Общий знаменатель  nx(х—2) (х+2). После упрощений получим уравнение

х2— (2—п) х— (2n2 + 4n) = 0,

Ответ   x1= n+2;    x2 =—2n.

__________________________________________________

398.

Первый   способ.   После обычных    преобразований   получаем уравнение

х2+ (а—2п—2а+п) х—(а—2п) (2а — n) =0.

Решение последнего уравнения можно найти сразу, если обратить внимание на то, что свободный член есть произведение величин —(а—2п) и (2а — n), а коэффициент при х есть сумма тех же величин, взятая с противоположным знаком.

Второй  способ.  Переносим единицу из правой части в левую, получим:

или

отсюда: 1) а —2n + х = 0 или   x1 = 2n — а,

2)  или x2= 2а — п.

Ответ x1 = 2n — а ; x2= 2а — п

__________________________________________________

399.

Получаем уравнение

(n—1)2x2—а (n—1) x + (а—1)=0;

чтобы избежать действий с дробями, можно положить (n—1) х = z или непосредственно найти (n—1) х  из уравнения

[(n—1) х ]2—а [(n—1) х ] + a — 1=0.

Получим

(n—1) x1 = a—1;     (n—1) x2 =1,

Ответ

__________________________________________________

400.

Знаменатель левой части равен (а — х)2. Помножив на него обе части уравнения, найдем

Извлекая корень, получаем одно из двух уравнений:

Ответ  

__________________________________________________

401.

Преобразуем сначала выражение

( l +ах)2— (а+х)2 = 1+ а2x2 — а2—х2.

Группируя в правой части первый член с последним, а второй c третьим, получаем
(1— х2) (1—а2). Теперь заданное уравнение приводится к виду

Ответ  

__________________________________________________

 
Используются технологии uCoz