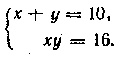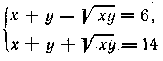|
|
ГЛАВА 3 АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ Ответы и решения В задаче 467 и в большинстве следующих задач этой главы применение искусственных приемов совершенно необходшло для их успешного решении. Основная трудность этих задач в том, чтобы подметить особенности данной системы и подыскать соответствующий искусственный прием. Можно решить по способу подстановки (из второго уравнения найти у = 6 — х или х = 6— у и подставить в первое). Несколько быстрее ведет к цели следующий искусственный прием. Первое уравнение преобразуется к виду (х—у)2=4, откуда х—у =2 или х—у = —2. Получаем две системы:
Ответ 1) x1 = 4, у1 = 2 2) x2 = 2, у2 = 4 __________________________________________________ Представим данную систему в виде
Положим для краткости xy = z1; x + y = z2. Тогда имеем систему
По теореме Виета z1 и z2 — корни квадратного уравнения z2 — 11z + 30=0. Находим: z1= 6, z2=5 или z1= 5, z2=6 . Получаем две системы:
К каждой можно снова применить теорему Виета (или решить по способу подстановки). Ответ 1) x = 5, y = 1 2) x = 1, y = 5 3) x = 2, y = 3 4) x = 3, y = 2 __________________________________________________ Положим y2 = z; тогда имеем систему
Ответ 1) х = 4, y = √3 2) х = 4, y = — √3 3) х = 3, у = 2. 4) х = 3, у = — 2. __________________________________________________ Положим х2 = z1 и — y = z2. Получим систему
Ответ 1) х = 5, y =2; 2) х = — 5, y = 2; 3) х = i√2 , y =—25; 4) х = — i√2 , y = —25.
__________________________________________________ Полагаем — ху = z1 ; х2 — у2 = z2 . Получим систему
Находим z1 = 9; z2 = —20 или z1 = —20; z2 = 9. Теперь имеем две системы:
Решим первую систему. Из первого ее уравнения находим у = —9/x. Подставляем во второе. Находим биквадратное уравнение х4 + 20х2 — 81=0. Его корни
Теперь находим
Тем же способом решаем вторую систему. Ответ 1) х ≈1,86, у ≈ — 4,84; 2) х ≈ —1,86, у ≈ 4,84; 3) х ≈ 4,84i, у ≈ 1,86i; 4) х ≈ — 4,84i, у ≈ —1,86i; 5) х = 5, у = 4; 6) х = — 5, у = —4; 7) х = 4i, у = —5i; 8) х = —4i, у = 5i. __________________________________________________ Исключим свободные члены, для чего помножим второе уравнение на 7 и вычтем из первого. Получим —32х2— 2ху + 75y2 = 0. Это — однородное уравнение второй степени (т. е. уравнение, содержащее только члены второй степени; членов первой степени и свободного члена в нем нет). Разделив обе части уравнения на х2 (это можно сделать, так как х = 0 не есть корень), мы преобразуем его к виду Теперь решаем две системы:
(по способу подстановки). Ответ __________________________________________________ 1-е уравнение запишем так: х2 — 2ху + у2 = 1/2 ху . Тогда имеем (х—у)2 = 1/2 ху 2-е уравнение запишем в виде 2(х—у) = 1/2 ху Значит, (х—у)2—2(х—у) = 0. Отсюда находим х—у = 0 и х—у = 2. Получаем две системы:
Ответ 1) х = у = 0; 2) х = 4, у = 2 3) х =— 2, у =—4. __________________________________________________ Первое уравнение перепишем так: (х2 + 2ху + у2) =13 + ху или (х + у)2— 13 = xy. Из второго уравнения х + у = 4; подставив, получим 16 —13 = xy. Решаем теперь систему
Ответ 1) х = 3, у =1; 2) х= 1, у = 3. __________________________________________________ Решается, как предыдущая задача. Получим новую систему
Ответ 1) х = 3, у = 2 2) х = — 3, у = —2 __________________________________________________ Полагаем х/у = z; тогда у/x = 1/z, и первое уравнение примет вид z + 1/z = 25/12 или 12z2—25z +12 = 0. Его корни z1 = 4/3 и z2 = 3/4 Теперь имеем две системы:
Системы решаются подстановкой значения х из первого уравнения во второе. Ответ 1) х = 4, y =3; 2) х = — 4, y = —3; 3) х = 3i, y = 4i; 4) х = —3i, y = —4i. __________________________________________________ Систему можно записать в виде
Перемножаем эти уравнения и делим одно на другое. Получаем
Перемножая эти уравнения, находим
Выраженне для y2 можно найти ачалогично, взяв уравнение Ответ
__________________________________________________ Во втором уравнении разлагаем х3 +у3 на множители (х + у)(х2 — ху + у2 ) и делим второе уравнение на первое. Получим х + у = 5. В первом уравнении прибавляем к правой и левой частям уравнения по 3ху; получим (х + у)2=7+3ху. Подставив 5 вместо (х + у) согласно полученному уравнению, найдем ху = 6. Теперь решаем систему
Ответ 1) х = 3, у = 2; 2) х = 2, у = 3. __________________________________________________ Помножим второе уравнение на 3 и сложим с первым. Получим (х + у)3=1, Если ограничиться действительными решениями, то отсюда х + у =1. Заменяя во втором уравнении х + у через 1, имеем ху = —2. Решаем систему
Ответ 1) х = 2, у = —1; 2) х =—1, у = 2.
__________________________________________________ Решается, как предыдущая задача. Ответ 1) х = 3, у = 2; 2) х = 2, у= 3. __________________________________________________ Полагаем Отсюда z = 5 и z = 1/5, т. е
Из уравнения Ответ 1) х = 3, у = 2; 2) х =— 3, у = —2; 3) х = 3i, у =—2i; 4) х = —3i, у =2i.
__________________________________________________ Исключаем из системы неизвестное z : второе уравнение вычитаем из первого, умноженного на с, третье уравнение вычитаем из второго, умноженного на с. Получим систему
Отсюда находим х и у. Аналогично находим z. Ответ __________________________________________________ Исключаем сначала и; для этого: 1) второе уравнение умножим на 2 и прибавим к первому; 2) третье уравнение умножим на (—2) и прибавим ко второму; 3) третье уравнение умножим на (—3) и прибавим к четвертому. Получим систему
Из этой системы исключим х, предварительно вычитая из второго уравнения третье. Получим
Складываем уравнения а) и в), а уравнение б) умножаем на 5 и складываем с в). Получим
Отсюда находим z =3 и у =2. Из уравнения б) находим х и из третьего заданного уравнения находим и. Ответ х =1; у =2; z =3; и = 4. __________________________________________________ Вычитаем из второго уравнения первое. Получим у + 2z =1. Отсюда у =1—2z. Подставляем это значение у в первое уравнение, находим х = z + 3. Подставляем найденные значения х и у в третье уравнение, получим 3z2 + z — 2 = 0. Корни его z1 = 2/3 и z2 = — 1. Подставляя значения z в уравнения x = z + 3 и у =1—2z, найдем по два значения х и у. Oтвет 1) x = 11/3, у = — 1/3, z = 2/3; 2) x = 2, у = 3, z = —1. __________________________________________________ Первое уравнение возводим в квадрат, второе — в куб и третье — в квадрат после переноса второго члена в правую часть уравнения. Получим систему
Ответ __________________________________________________ Возводим первое уравнение в квадрат и вычитаем второе. Получаем ху + хz + уz = 54. В силу третьего уравнения можно заменить первые два слагаемых через 2уz. Получаем 3yz = 54, т. е. yz =18. (а) Теперь третье уравнение можно записать в виде xy + xz = 2•18, т. е. x( у + z) = 36. (б) A так как первое уравнение имеет вид х + ( у + z) = 13. (в) то из уравнений (б) и (в) можно найти х и y + z. Получаем:
Чтобы найти у и z по отдельности, присоединим уравнение (а). Получим две системы:
Замечание. При возведении в квадрат первого уравнения возникает опасность появления лишних решений. Но если бы они появились, то удовлетворяли бы уравнению х + у + z = —13, что противоречило бы уравнению (в) Ответ. 1) х = 9, у = 2 + i √14 , z = 2 — i √14 ; 2) = 9, у = 2 — i√14 , z = 2 + i √14 3) х = 4, у=6, z=6. 4) х =4, у = 3, z =3;
__________________________________________________ Третье уравнение представим в виде z2 — xz — yz + xy = 2. Сложив его со вторым, получим z2 + 2xy =49. (a) Отсюда z2 = 49—2xy. Подставляем это выражение в первое уравнение. Получим (х + у )2 =4 9, т. е. х + у= ±7. Положим сначала х + у = 7. Представим второе уравнение в виде xy + z(x + y)=47 . и сюда подставим выражениеху значение х + у = 7. Получаем z2—14z + 45=0. Отсюда z1 = 5 и z2 = 9. Если z = 5, то Имеем две системы:
каждая из которых имеет по два решения. Всего получаем четыре решения:
Теперь положим х + у = —7 и тем же способом найдем еще четыре решения. Ответ
__________________________________________________ Вычитаем сначала второе, а затем третье уравнение из первого. Получаем:
Сокращаем уравнение (а) на (а—b) и уравнение (б) на (а—с). Имеем:
Вычитаем (г) из (в). Получаем
Отсюда . Неизвестное у находим из (в) или из (г). Теперь по любому из данных уравнений найдем z. Ответ __________________________________________________ Положим
Ее корни
Отсюда находим х =17; у = 6. Ответ х =17; у = 6. __________________________________________________ В силу второго уравнения первое можно записать так: 10 — 2√xy = 4. Отсюда ху = 9. Получаем систему
Oтвет 1) х = 9, y = 1; 2) х =1, y = 9. __________________________________________________ Полагаем Ответ 1) х = 6, y =12; 2) х = —4,5, y = —9. __________________________________________________ Первое уравнение приводится к виду х2 + у2=136. (а) Второе уравнение возводим в квадрат; получим у2 = 36х—324. (б) Это выражение подставляем в (а). Получаем х2 + 36х —460 = 0. Отсюда находим х=10 и х = —46. Подставляя в (б), находим у. Получаем четыре пары решений: 1) х =10, у = 6; 3) х =— 46, у = 6√55 ; 2) х =10, у = —6; 4) х =— 46, у = —6√55 . Третья и четвертая пары решений не годятся, так как выражения √х + у и √х — у , где радикалы должны означать арифметические значения корня (в противном случае они неопределенны ввиду двузначности корня), не имеют смысла при комплексных значениях х + у и х—у. Первую и вторую пару решений следует проверить. Ответ 1) х =10, у = 6; 2) х =10, у = — 6.
__________________________________________________ Система имеет смысл только при а > 0 (см. предыдущее объяснение). Первое уравнение возводим в квадрат:
Это выражение подставляем во второе уравнение; получаем
Возводим в квадрат уравнения (а) и (б): у2 = 64а2+16ах, (а') у2 = (√41 + 5)2 а2— 2(√41 + 5)ax. (б') Исключая у из (а') и (б'), получаем (130+ 10√41 ) а2 = (26+ 2√41 )ax откуда х =5а. Из (а') находим y = ±4а и затем производим проверку. Ответ 1) х =5а, у =4а; 2) х =5а, у =—4а. __________________________________________________ Возводим первое уравнение в квадрат; 2х2—2√х2 — у2 = у2. Подставляем сюда значение х4—у4 = 144а4 из второго уравнения. Получаем у2=2х2—24а2. (а) Отсюда находим у4 и подставляем во второе заданное уравнение. Получаем х4—32а2х2+240а4 = 0. Отсюда х = ±√20 а и х = ±√12 а. Из уравнения (а) находим у. Для каждого из значений х = ±√20 а имеем у = ±4а, а для каждого из значений х = ±√12 а имеем, у =0. Проверка показывает, что из полученных шести пар решений одни являются лишними при а > 0, другие же являются лишними при а < 0. Возьмем, например, пару решений х = √20 а, у = 4а. Подставляя в первое уравнение, мы находим √36а2 —√4а2 = 4а, т. е. 6|а|—2|а|=4а. Это равенство является тождеством при а > 0, но оно не верно при а < 0. Ответ. При а > 0 решения будут: 1) х = √20 а, у = 4а; 2) х = — √20 а, у = 4а 3) х = √12 а, у = 0; 4) х = — √12 а, у = 0. При а < 0 решения будут: 5) х = √20 а, у = — 4а 6) х = —√20 а, у = — 4а. __________________________________________________ Первый способ. Из второго уравнения находим х + у = 14 —√ху . Возводим в квадрат; получаем x2 + y2 + 2xy = 196 + xy —28 √ху, откуда x2 + y2 + xy = 196 —28 √ху. В силу первого уравнения имеем 84 = 196 —28 √ху. Отсюда находим √ху = 4, т. е. xy=16. Подставляя во второе уравнение значение √ху = 4, находим x + y =10. Решаем систему
Второй способ. Левую часть первого уравнения разлагаем на множители: x2 + y2 + xy = (x + y)2 — ( √ху)2= (x + y + √ху) (x + y — √ху) = 84. Отсюда в силу второго уравнения получаем 14(x + y — √ху) = 84, т. е. x + y — √ху = 6. Из системы
можно найти х + у и √ху. Ответ. 1) х = 2, у = 8; 2) х = 8, у = 2.
__________________________________________________ Из первого уравнения находим приравняв эти два выражения, получаем (1+т)x2 + (2 + т)x + (2—т) = 0. Это уравнение имеет действительные корни при условии (2 + т)2—4(1+ т)(2—т) >0. После упрощения левой части получим выражение 5т2—4 > 0, откуда Ответ
__________________________________________________ |
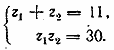
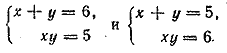
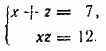
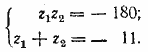
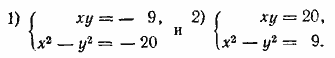
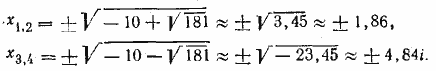
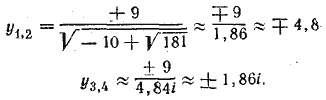
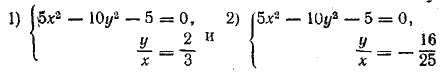
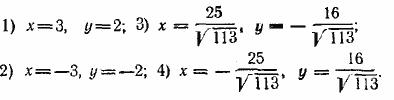
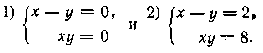
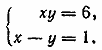
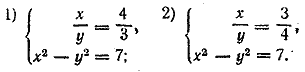
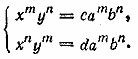
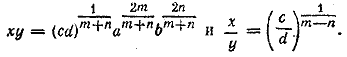
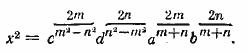
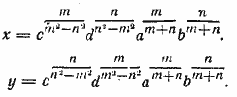
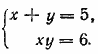
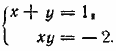
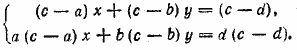
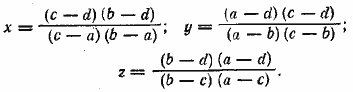
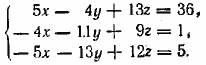
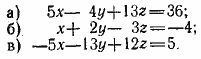
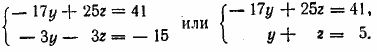
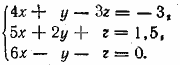
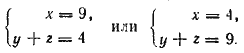
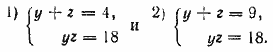
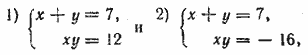
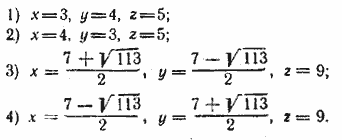
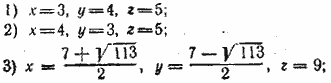
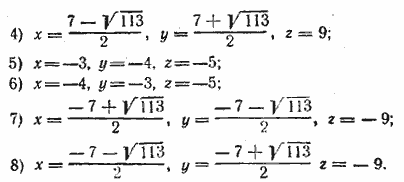
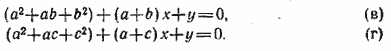
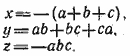
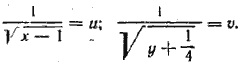 . Получаем систему
. Получаем систему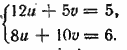
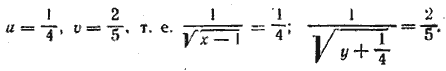
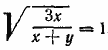 . Из последующего уравнения находим у = 2х и подставляем во второе уравнение.
. Из последующего уравнения находим у = 2х и подставляем во второе уравнение.