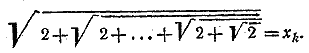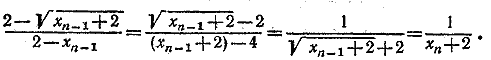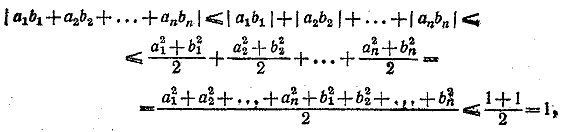|
|
ГЛАВА 5 НЕРАВЕНСТВА Ответы и решения
Для того чтобы квадратный трехчлен ax2 + bx + c (а=/=0) был положителен при всех х, необходимо и достаточно, чтобы а > 0 и дискриминант D трехчлена был отрицателен. В нашем случае имеем а = r2 — 1 > 0; (1) D = 4(r —1)2—4(r2 — 1)= — 8(r — 1) < 0. (2) Неравенства (1) и (2) одновременно выполняются при r > 1. Заметим еще, что при r =1 рассматриваемый в задаче многочлен тождественно равен 1. Таким образом, все искомые значения r определяются неравенством r > 1 __________________________________________________ Если положить 3и2—8и + 4. (1) Если х и у разных знаков, то и < 0 и трехчлен (1) положителен. Если же х и у одного знака, То легко Видеть, что и >2. Так как корни квадратного трехчлена (1) равны 2/3 и 2, то при и >2 трехчлен неотрицателен. Таким образом, трехчлен неотрицателен при и < 0 и при и >2, а следовательно, исходное выражение неотрицательно при всех вещественных х и у , не равных нулю. __________________________________________________ Заметим, что х2— х + 1 > 0 при всех значениях х, так как дискриминант квадратного трехчлена равен —3 < 0 и коэффициент при х2 положителен; мы вправе поэтому умножить оба неравенства на знаменатель. В результате получим: 3х2 + 3х —3 < х2 + ах—2, х2 + ах—2 < 2х2— 2х + 2, или 4х2 + (а—3)х +1 >0, х2 — (а + 2)х+4> 0. Первое неравенство справедливо при всех х тогда и только тогда, когда дискриминант квадратного трехчлена меньше нуля, т. е. когда (а—3)2 —16 < 0. По аналогичной причине второе неравенство выполняется при условии (а + 2)2 —16 < 0. Решая теперь совместно два неравенства (а—3)2 —16 < 0 и (а + 2)2 —16 < 0 относительно а, получаем: —4 < а—3 < 4, —1< а <7 и —4 < а + 2 < 4, — 6 < а < 2. Отсюда окончательно имеем — 1 < а < 2. __________________________________________________ В силу неравенства (1) предварительных замечаний имеем а4+b4 > 2a2b2, c4+d4 > 2c2d2. Складывая эти неравенства, получаем а4+b4+ c4+d4 > 2 (a2b2 + c2d2). (1) Согласно неравенству (3) предварительных замечаний , полагая u = a2b2 и v = c2d2, имеем a2b2 + c2d2 > 2 √a2b2c2d2. (2) Так как всегда √a2b2c2d2 > abcd (знак > в случае, если abcd < 0)s то сопоставляя (1) и (2), приходим к доказательству предлагаемого неравенства. __________________________________________________ Данная система равносильна следующей: x2+ (x+а)2 + 2x < 1, у = х + а. Неравенство 2x2 + 2(а+1)x + a2 —1< 0 имеет единственное решение относительно х тогда и только тогда, когда дискриминант трехчлена равен нулю: (а+1)2—2 (а2—1) = 0, т. е. a2—2a — 3 = 0; отсюда a1 = 3, a2 = —1. 1) Если а = 3, то x2 + 4x + 4 = 0 и х = — 2, у =1. 2) Если а =— 1, то x2 = 0 и x =0, у = —1. __________________________________________________ Запишем данную систему неравенств следующим образом: y + 1/2 > |х2 — 2х|, у < 2—|х—1|. Так как всегда х2 — 2х| > 0 и |х—1|> 0, то —1/2 < у < 2 Единственными целыми числами у, удовлетворяющими этому неравенству, являются 0 и 1. Следовательно, данная система неравенств, рассматриваемая для целых х и у, может быть совместна лишь при значениях у = 0 и у=1. Рассмотрим оба случая. Случай 1. Если у = 0, то система неравенств принимает вид |х2 — 2х| < 1/2, |х—1| < 2. Второму из этих неравенств удовлетворяют лишь целые числа: 0, 1 и 2. Подстановкой нетрудно убедиться, что 0 и 2 удовлетворяют и первому неравенству, а 1 ему не удовлетворяет. Итак, для случая у = 0 найдены два решения: x1 = 0, y1 = 0; x2 = 2, y2 = 0 Случай 2. Если у = 1, то исходная система неравенств приводит к следующей: |х2 — 2х| < 3/2, |х—1| < 1. Второму из этих неравенств удовлетворяет единственное целое число х = 1, которое удовлетворяет и первому из неравенств. Итак, в этом случае имеем еще одно решение задачи: x3 = 1, y3 = 1. Таким образом, система неравенств удовлетворяется тремя парами целых чисел. __________________________________________________ В левой части всего п слагаемых, причем первые п — 1 слагаемых строго больше последнего. Поэтому
__________________________________________________ Обозначим через Sm левую часть доказываемого неравенства. Легко видеть, что при этом
Приведя дроби к общему знаменателю, найдем:
Таким образом, Sm+1> Sm. Так как
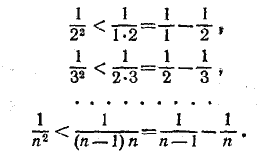
то, следовательно, Sm> Sm— 1 > ... > S2 > S1 > 1, т. е. Sm > 1, что и требовалось доказать. __________________________________________________ Напишем ряд очевидных неравенств:
Сложив эти неравенства почленно, получим:
что и требовалось доказать.
__________________________________________________ Перепишем обе части доказываемого неравенства следующим образом:
Докажем, что (n—k + l)k > n (1) при n > k > l. Действительно, nk—k2+ k—n = k(n—k) — (n—k) = (n—k)(k —1) > 0. (2) Таким образом, мы уже доказали, что (n!)2 > nn. (3) Заметим, что если число k больше единицы и меньше, чем п, то в формуле (1), как это следует из (2), имеет место строгое неравенство. Оно, очевидно, повлечет за собой строгое неравенство и в формуле (3). При п > 2 такое число k найдется. Следовательно, в этом случае справедливо строгое неравенство (n!)2 > nn __________________________________________________ Легко проверить, что для построения треугольника со сторонами а, b, с необходимо и достаточно, чтобы эти числа а, b, с , удовлетворяли трем неравенствам:
Докажем, что одновременное выполнение этих неравенств эквивалентно выполнению поставленного в задаче условия. Положим K = pa2 + qb2 — pqc2. Так как q = 1—p, то предыдущее выражение можно переписать в виде K = pa2+(1—p)b2—р(1—p)c2 = c2p2+(a2—b2—c2)р + b2, где а, b, с—постоянные, a p может принимать любые значения. Таким образом, К представляет собой квадратный трехчлен относительно р. В общем случае, в зависимости от величины р, трехчлен К может принимать значения разных знаков. Указанное в задаче неравенство равносильно тому, что К > 0 при всех р. Для этого, как известно, необходимо и достаточно, чтобы дискриминант трехчлена D = (a2—b2—c2)2 — 4b2c2 был отрицателен (мы учли при этом, что коэффициент при p2 равен c2 > 0). Дискриминант можно представить в следующей форме:
Если треугольник можно построить, то неравенства (1) выполнены и, следовательно, D < 0. Тем самым в одну сторону утверждение доказано. Обратно, если D < 0, то (а + b—с) (b+с—а) (с+а—b) > 0. (2) Покажем, что отсюда следуют все три неравенства (1). Действительно, предположим, что только одна из скобок в левой части (2) положительна, а две другие отрицательны, например а + b—с < 0 и b+с—а < 0. Сложив эти неравенства, получим 2b < 0, что невозможно. Таким образом, утверждение доказано и в другую сторону. __________________________________________________ Преобразуем левую часть неравенства следующим образом: 4(x+y)(x + z)x(x+y+z) + y2z2 = 4(х2 + ху + хz + уz)(х2+ху+хz)+ y2z2 = = 4(х2+ху+хz)2 + 4yz(х2+ху+хz)+y2z2 = [2 (х2+ху+хz) + yz]2 Полученное выражение неотрицательно при любых вещественных x, у, z, что и требовалось доказать. __________________________________________________ Обозначив левую часть неравенства через z, преобразуем z следующим образом: z = х2+2ху + 3y2 + 2х + 6у + 4 = (x + y +1)2 + 2(y+1)2+1. При вещественных х и у первые два слагаемых неотрицательны, а значит, z > 1. __________________________________________________ Так как
которое легко преобразуется к следующему очевидному: 100у2 — 40у + 4 = (10у—2)2 > 0. __________________________________________________ Так как d > 0 и R > 0, то d 2+ R2 — r2>0 и 2dR > 0. Следовательно, данное неравенство равносильно неравенству d 2+ R2 — r2 < 2dR. Приведя его к виду (d—R)2 < r2, получим |d—R|< r или — r < d—R < r. Следовательно, R—r < d < R + r.
__________________________________________________ Умножив обе части доказываемого неравенства на a+b+c, получим равносильное неравенство, левая часть которого равна
__________________________________________________ Заметим, что данное выражение обращается в нуль при b = с, с = а, а = b. Поэтому по теореме Безу оно делится без остатка на разности a —b, а—с, b—с. Расположив слагаемые по убывающим степеням буквы а, получим, проведя деление нa a —b: а3(b2—с2) + а2(с3—b3) + b3с2—с3b2 = = (а—b) [а2 (b2—с2) + ас2 (с—b) + bс2 (с—b)]. Вынесем далее из выражения, стоящего в квадратных скобках, множитель (b—с) и оставшийся многочлен разделим на а—с. В результате получим а3 (b2—с2) + b3 (с2—a2) + с3 (a2—b2) = = — (b—а) (с—b) (с—а) (ас+bс+ab). Так как по условию а < b < с и а, b, с одного знака, то выражение справа отрицательно. __________________________________________________ Имеем: 1—2 √ak+ ak = (1 —√ak)2>0, откуда 1 +√ak >2 √ak Написав эти неравенства для k = l, 2, ... и перемножив их почленно, получим: (1+a1)(1+a2)...(1+an) > 2n √a1a2...an=2n.
__________________________________________________ Достаточно рассмотреть случай, когда а и b одного знака (т. е. положительны), так как в противном случае одно из чисел больше 1 и неравенство очевидно. Имеем: а2+b2 = (а+b)2 — 2аb = 1 — 2ab, а4+b4 = (1 — 2аb)2 — 2a2b2. Но если а+b = 1, то 0 < аb <1/4, так как
(см. формулу (3) предварительных замечаний ). Следовательно,
__________________________________________________ Рассмотрим три случая: 1) x <0; тогда x8 — x5 + x2— x + 1 > 0, ибо первые четыре слагаемых неотрицательны; 2) 0 < х < 1; преобразуем многочлен к виду x8 + (x2—x5 ) + ( 1— х) = x8 + x2 (1— x3) + (1— x). Здесь все слагаемые, очевидно, положительны, следовательно, и многочлен больше нуля; 3) x > 1; запишем многочлен в виде x5 (x3—1 ) + x(x—1 ) + 1. Первые два слагаемых неотрицательны; следовательно, и в этом cлучае x8 — x5 + x2— x + 1 > 0. __________________________________________________ Имеем:
причем последнее слагаемое суммы, стоящей в скобках, равно xn, если n четно, и пхn—1, если п нечетно. По условию —1 < х < 1, откуда следует, что (1 + х)n + (1—х)n < An где An—значение многочлена (1) при х = ± 1, т. е. An=2n. __________________________________________________ Доказываемое неравенство равносильно неравенству
которое справедливо, так как левая часть равна
__________________________________________________ Подкоренное выражение должно быть > 0, поэтому —1/2<x < 1/2. (1) При значениях х, удовлетворяющих условию (1) и не равных нулю, √1—4х2 < 1. Поэтому, если —1/2<x < 0, то указанное в задаче неравенство выполняется, ибо левая часть его отрицательна. Если же 0< x < 1/2, то, освободив в левой части неравенства числитель от иррациональности, получим
Легко видеть, что числитель дроби, стоящей справа, при 0< x < 1/2 не превосходит 2, а знаменатель >1. Поэтому
Итак, предлагаемое неравенство справедливо для значений х =/= 0 и удовлетворяющих условию (1). При х = 0 и |х|>1/2 левая часть неравенства теряет смысл. __________________________________________________ Пусть для определенности х > у. Тогда полагая y/x = α<1, получим равносильное неравенство m√1 + αm > n√1 + αn Возведя обе части (1) в степень тп, придем к неравенству ( 1 + αm )n > ( 1 + αn )m Легко видеть, что это неравенство справедливо, ибо 0<α<1, a n > m
__________________________________________________ Положим
Легко видеть, что х2— х—а<0. (2) Корни трехчлена, стоящего слева, равны
Так как числа xn удовлетворяют неравенству (2), то все они заключены между корнями x(1) и x(2)(см. предварительныe замечания ). Следовательно,
что и требовалось доказать. При п=1 имеем x1 = √a и неравенство (3) очевидно.
__________________________________________________ Обозначим выражение, содержащее k знаков радикала, через xk
Заметим, что xk < 2. В самом деле, заменим под знаком последнего внутреннего радикала 2 на 4. В результате все корни последовательно извлекутся и левая часть окажется равной 2. Значит, xk< 2. Отсюда, в частности, следует, что числитель и знаменатель в левой части исходного неравенства отличны от нуля. Пользуясь далее тем, что
преобразуем левую часть исходного неравенства следующим образом:
Так как
__________________________________________________ Как известно, для любых вещественных чисел а и b имеет место неравенство
Пользуясь далее тем, что абсолютная величина суммы не превосходит суммы абсолютных величин соответствующих слагаемых, получаем:
что и требовалось доказать. __________________________________________________ Если n =1то x1= l и( следовательно, x1> l так что утверждение верно. Пусть оно верно для всех т, где 1 < m < п—1 докажем справедливость для т = п. Если все числа x1, x2, ... xn равны единице, то утверждение справедливо. Если хотя бы oдно из этих чисел больше единицы, то в силу равенства x1x2 ... xn =1найдется другое, меньшее единицы. Пусть нумерация такова , что xn > 1, xn—1< 1. Из предположения индукции и условия x1x2 ... xn—2 (xn—1xn) = 1 следует: x1+ x2 + ... + xn—2 + xn—1xn > n — 1 т. е. x1+ x2 + ... + xn—2 + xn—1xn + l > n Так как (xn— 1) (1—xn—1) > 0, то xn + xn—1 — xnxn—1 — l > 0 и, следовательно, xn—1+ xn > xn—1 xn + l Таким образом, x1+ x2 + ... + xn—1 + xn > x1+ x2 + ... + xn—2 + xn—1xn + l > n и утверждение доказано. __________________________________________________
|
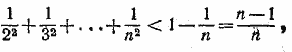
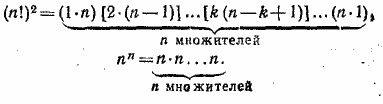
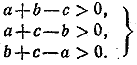 (1)
(1)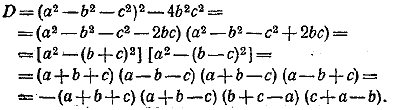
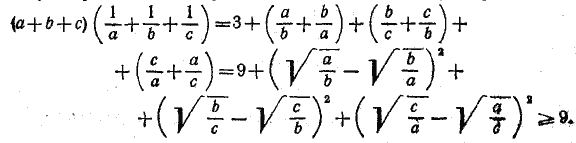
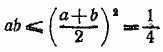
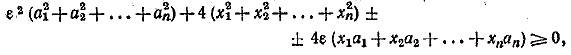

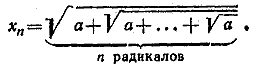 (1)
(1)