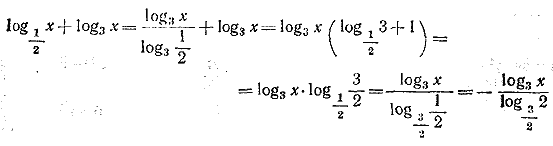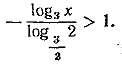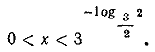ГЛАВА  5

НЕРАВЕНСТВА

Ответы и решения

613.

Пользуясь  логарифмическим   тождеством   , преобразуем левую часть данного   неравенства   следующим   образом:

Тогда данное неравенство примет вид

Так  как 2 > 1   и ³/₂ > 1 и по свойству   логарифмов , то, следовательно, предыдущее неравенство эквивалентно неравенству

Отсюда, заметив еще, что по смыслу задачи х > 0, окончательно получаем:

__________________________________________________

614.

  Так как x > 0,   то данное  неравенство  равносильно  неравенству

Но а > 1, поэтому, логарифмируя последнее неравенство по основанию а (эта операция также приводит к равносильному неравенству), получим:

Отсюда окончательно находим!

либо  log_ax > √2 и, следовательно,  

либо  log_ax < — √2 , и тогда

__________________________________________________

615.

 По   смыслу   задачи   х > 0,   поэтому   данное   неравенствo  равносильно неравенству

log_ax(x + l) <  log_a(2х + 6).

Так как а > 1, то отсюда    x (x + l) <  (2х + 6), или

x²—x—6 < 0.

Решая это квадратное неравенство при условии х > 0, получаем

0 < х < 3.

__________________________________________________

616.

Предлагаемое неравенство равносильно следующему

0< x² — 5x + 6 < 1.

Так как   x² — 5x + 6 = (х—2) (х—3),   то   неравенство   0 < x² — 5x + 6  справедливо при

х < 2   и   х >3.

Решая  далее  неравенство   x² — 5x + 6 < 1,   находим,   что  оно   выполняется при

Так как √5 > 2, то    .   Поэтому исходное неравенство имеет место при

__________________________________________________

617.

  Приведя левую часть к общему знаменателю, находим

Так как числитель последнего выражения положителен   [ в самом деле,

], то   неравенство  сводится к следующему

log₂x (log₂x — 1) > 0.

Это последнее неравенство выполняется  при х > 2 и при 0 < х < 1.

__________________________________________________

618.

По   смыслу   задачи х > 0 и,   значит,   данное   неравенство равносильно неравенству

Прологарифмируем это неравенство по основанию 2 и положим у = log₂x ; получим равносильное неравенство

у(3—у²— 2у) >0,

которое после разложения квадратного трехчлена на множители можно записать в виде

у(1—у)(3 + у) >0.

Это неравенство выполнено тогда и только тогда, когда либо все три семножителя положительны, либо один из них положителен, а два других отрицательны. В первом случае, т. е. когда

у > 0,    1—у > 0,      3 + у > 0,

находим 0 < у < 1 и, следовательно,

1 < х < 2.                                            (1)

Втерой случай подразделяется на три подслучая, причем непротиворечивая система неравенств получается только в одном подслучае, а именно когда

у < 0,      1 — у > 0,      3 + у < 0.

Отсюда у < —3 и, значит,

0 < х < ¹/₈.                                          (2)

Таким образом, исходное неравенство имеет место тогда и только тогда, когда либо

0 < х < ¹/₈,

либо

1 < х < 2.

__________________________________________________

619.

Положив log₂x  = y  и  заметив,   что перепишем данное неравенство в виде

y +  ¹/_y + 2cosα  < 0.                                    (1)

Число    z = y +  ¹/_y    имеет тот же знак, что и число у, и | z | > 2 при всех у (см. (2), предварительные замечания).

Поэтому если z  > 0, то неравенство    z <  — 2cosα    может быть выполнено только в том случае, если z = 2 (у=1) и  cosα = — 1,   т.  е. если  в исходном  неравенстве  х = 2 и

α = (2k+l)π    (k = 0,  ±1,  ±2, ...). При этих значениях имеет место знак равенства.

Если же z < 0, т. е. у < 0, то z < — 2 и неравенство (1) выполнено при всех α, откуда следует, что исходное неравенство выполняется, кроме уже найденных значений, при 0 < х < 1 и всех вещественных значениях α.

__________________________________________________

620.

Исходное неравенство равносильно следующему

0< log₄ (x² — 5) < 1,

откуда 1 < x² — 5 < 4 или 6 < x²  < 9 или  √6  < | х | < 3.

Ответ: √6  <  х  < 3  и  — 3 < х < — √6

__________________________________________________