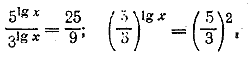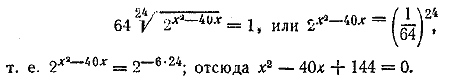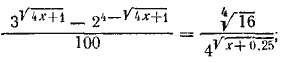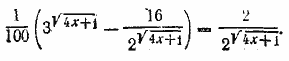|
|
ГЛАВА 4 ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ, ТОЖДЕСТВА. Ответы и решения
Первый способ.
Согласно определению логарифма Отв. х =22,5. Второй способ. Логарифмируя, будем иметь
Отв. х =22,5.
__________________________________________________ Как в задаче 497(второй способ), будем иметь
Отв. х =5.
__________________________________________________ Поступая, как в предыдущих задачах, будем иметь
Отв. x =20.
__________________________________________________ Первый способ.
(ср. с решением задачи 497 по первому способу). Второй способ. Обозначим Логарифмируя, находим, что log7 y =(1 — log7 2) log7 49, или
откуда у = 49/4 аналогично найдем, что z = 1/4. Следовательно , x = 25/2 Oтв. x = 25/2
__________________________________________________ Имеем log4 log3 log2 x = log4 l, откуда log3 log2 x = l ; log2 x=3. Отв. х = 8.
__________________________________________________ Аналогично решению предыдущей задачи имеем.
далее
Отв. х=1. __________________________________________________ Выражение в фигурных скобках должно быть положительным числом, так как отрицательное число не имеет (действительного) логарифма при основании 4. Поэтому, переписав данное уравнение в виде
мы должны взять только положительное значение √4 ,т. е. 2. Применяя аналогичные преобразования повторно, получим далее
следовательно, 1+3log2 х =4, log2 х =l. Отв. х = 2. __________________________________________________ Данное уравнение представим в виде log2 (x+14) (x+2)=6, или (x+14) (x+2)=26 = 64, откуда имеем x2+16x—36=0, x1 = 2, x2 =—18. Второй корень не годится, так как в левую часть входят выражения log2 (x+14) и log2 (x+2), которые при отрицательном х не имеют действительного значения. Отв. х = 2.
__________________________________________________ Представим данное уравнение в виде logа[ у(у+ 5) • 0,02]=0; отсюда у(у+ 5) • 0,02=1 или у2+5у—50 = 0; получим два корня у1 = 5, у2=—10. Второй корень не годится (см. предыдущее решение). Отв. у = 5.
__________________________________________________ Имеем lg(35—x3) =3 lg (5—x) или lg(35—x3) = lg ( 5—x)3 следовательно, 35—x3= ( 5—x)3 или x2—5x+6 = 0. Отв. x1=5; x2 = —3; __________________________________________________ Преобразуя выражение в квадратных скобках, получим
Тогда- заданное уравнение примет вид
Применяя в правой части теорему о логарифме произведения (и дроби), получим 1 + lg x = lg(a—b)—lgb. Заменяя единицу через lg 10, перепишем уравнение в виде oтсюда Отв. __________________________________________________ Данное уравнение можно представить в виде
потенцируя, находим
__________________________________________________ Данное уравнение можно иначе записать так:
так как logx x = 1, то после упрощений получим Решая квадратное уравнение (с неизвестным logx 5), находим два корня: logx 5 = 5 и logx 5=1. Отв. x1 = 5√5 ; x2 = 5.
__________________________________________________ Первый способ. Положив log16 x = z, имеем х =16z отсюда log4 x = z log4 16=2z и log2 x = z log2 16= 4z. Данное уравнение примет вид z+2z+4z = 7, т. е. z =1. Второй способ. Приведем все логарифмы к основанию 2. По формуле (б) предварительные замечания находим: Отв. х =16. __________________________________________________ Решается, как предыдущая. Отв. х = а. __________________________________________________ Перепишем данное уравнение в виде
откуда 3х—7 = 3—7х. Отв. х = 1. __________________________________________________ Представим заданное уравнение в виде 7 •3х+1 — 3х+4 = 5х+2 — 5х+3. Вынося за скобку 3х и 5х, будем иметь 3х (7 • 3 — 34) = 5х (52 — 53), или (3/5)х = 5/3 откуда х= — 1. Отв х= — 1 __________________________________________________ Перепишем заданное уравнение в виде
Отсюда имеем 4х — 9 = 5/2 х. Отв. х = 6.
__________________________________________________ Заданное уравнение можно записать так:
Следовательно, —x2 +2x +2 = —6. Отв. x1 = 4; x2 = —2. __________________________________________________ Представим заданное уравнение в виде
Отв. x = 10.
__________________________________________________ Так как
Следовательно, 2х+3(1— х) = 1. Отв. x=2. __________________________________________________ Представим заданное уравнение в виде приравнивая показатели, находим
Введем обозначение √х = z; тогда будем иметь 2z2 — 5z — 3 = 0, откуда z1 = 3, z2 = —1/2. Но второй корень не годится, так как величина z (он представляет арифметическое значение корня √х ) должна быть положительной. Итак, имеем 3 = √х . Отсюда х = 9. Отв. х =9 __________________________________________________ Заданное уравнение можно представить в виде
Следовательно,
откуда имеем 3х —8 √х —3=0. Обозначив √х = z, будем иметь 3z2 — 8z — 3 = 0; z1= 3; z2 = —1/3 , второй корень z2 = —1/3 не годится (см решение задачи 518). Следовательно, х =9. Отв. х=9.
__________________________________________________ Данное уравнение можно записать так:
Следоиательно,
После упрощений получаем х2—2х—15= 0. Отв. х1= 5; х2= —3 __________________________________________________ Пользуясь формулой (а) предварительные замечания , получим Решаем относительно logха и получаем
__________________________________________________ По формуле (б) предварительные замечания найдем
Тогда данное уравнение примет вид log4 (х+12) =2 log4 х, откуда х+12= х2. Берем только положительный корень х=4; при отрицательном х выражение logх2 не имеет действительного значения. Отв. х = 4 __________________________________________________ Данное уравнение запишем так:
Так как
Решив его относительно log2 x, найдем
Отв. x1 = √5; x2 = 1/5
__________________________________________________ Левая часть уравнения есть сумма х+l членов геометрической прогрессии, а потому (в случае a=/=l) имеем
откуда ах + 1 = а16; х +1 =16; х =15. При а =1 общая формула суммы членов геометрической прогрессии неприменима, В этом случае левая часть данного уравнения есть сумма х+1 слагаемых, каждое из которых равно 1, так что уравнение принимает вид х +1 =16, и мы снова имеем х=15. Отв. х = 15.
__________________________________________________ Данное уравнение перепишем в виде 52+4+6+...+2x = 556 ,откуда 2+4+6+...+2x = 56, или 1+2+3+...+x = 28. Левая часть уравнения есть сумма членов арифметической прогрессии. Поэтому получаем уравнение
откуда x1 = 7, x2 = —8. Второй корень не годится, так как по смыслу задачи число х должно быть целым положительным. Отв. х=7. __________________________________________________ Заданное уравнение перепишем в виде 22x2—4—17 • 2x2—4+1= 0. Обозначая 2x = z, получим z2— 17z+16=0; z1=16; z2= 1, откуда x1 = 4; x2= 0. Отв. x1 = 4; x2= 0. __________________________________________________ Аналогично предыдущей задаче, полагая 4x =z, будем иметь 2z2—17z +8 = 0. Отв. x1 = 3/2; x2=— 1/2;
__________________________________________________ Полагая 3z2—10z+3=0. Отв.x1 = 2; x2 = — 2,
__________________________________________________ Логарифмируя данное уравнение (по основанию 10), получаем откуда lg x1 = l ; lg x2=— 4. Oтв. x1 = 10; x2=0,0001. __________________________________________________ Преобразуем данное уравнение так, чтобы каждая его часть представляла логарифм некоторого выражения. Для этого вместо 1 в левой части уравнения напишем lg 10. Теперь данное уравнение можно записать в виде
Из равенства логарифмов следует равенство чисел, т. е.
После упрощений получаем уравнение
Так как z2—5z—24=0. Корни этого уравнения z1= 8 и z2=—3. Взяв z1= 8, получаем уравнение Второй корень z=—3 приведет к уравнению Отв. х=36. __________________________________________________ Последовательно находим (см. решение предыдущей задачи):
отсюда
После упрощения получим
откуда Уравнение (А) можно было бы решить иначе. Уравнение (А) можно сократить на Отв. х = 9. __________________________________________________ Представим данное уравнение в виде 5lg x + 5lg x— 1 = 3lg x+ 1 + 3lg x— 1. Вынося за скобку 5lg x и 3lg x, будем иметь 5lg x(1+5— 1)=3lg x(3 + 3— 1), или
откуда lg х =2. Oтв. x = 100
__________________________________________________ Логарифмируя при основании 10, получим 2 1g4x — l,5 1g2x =1/2. Это биквадратное уравнение (относительно lg x) имеет два действительных корня: lg x= 1 и lg x =—1; следовательно, x1 = 10, x2=0,1. Отв. x1 = 10, x2=0,1.
__________________________________________________ Потенцируя, получим
Отв. x1 = 36, x2= 4. __________________________________________________ Согласно определению логарифма данное уравнение равносильно уравнению Отв. x1 = 3, x2= 0. __________________________________________________ Как в задаче 531, получим 2(4x— 2+ 9)=10(2x— 2 + 1). Заметив, что 2x— 2= 2x•2— 2= 1/4 • 2x, a 4x— 2= 4x•4— 2= 1/16 • 4x, получим уравнение 2 2х — 20 • 2х + 64 = 0, откуда, как в предыдущей задаче, найдем x1 = 4, x2= 2. Отв. x1 = 4, x2= 2. __________________________________________________ Последний член удобно перенести в правую часть. Затем, как в задаче 531 получим
Полагая z2—12z+27=0; корни его z1 = 9, z2= 3. Отв. x1 = 1/4, x2= 1/2. __________________________________________________ Потенцируя (ср. решение задачи 531), будем иметь
это уравнение можно представить в виде
Освобождаясь от знаменателя, получаем
откуда х =2 Отв. х=2. __________________________________________________ Представим данное уравнение в виде 4 lg2+2 lg (х—3)= lg (7х+ l )+lg (х— 6)+lg 3; потенцируя, находим: 22(х—3)2=3 (7х+1) (х—6). Корни этого квадратного уравнения суть x1 =9; x2=—3,6. Второй корень не годится, так как он дает х—3 =—6,6, значит, выражение lg (х—3) не имеет действительного значения [то же можно сказать и о выражениях lg (7х+ l ) и lg (х— 6)]. Отв. х = 9.
__________________________________________________ Правую часть представим в виде —log5 (0,2 —0,2 • 5x— 3) = — log5 0,2 — log5 (1 — 5x— 3). Слагаемое (х—3) представим в виде log5 5x— 3 После переноса членов получим уравнение log5120 + log55x— 3 + log5 0,2 = 2log5(1 — 5x— 3) — log5 (1 — 5x— 3), или 120 • 0,2 • 5x— 3 = 1 — 5x— 3. Отв. х = 1.
__________________________________________________
|
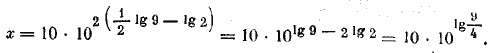
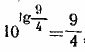 ,поэтому х = 10 • 9/4= 22,5
,поэтому х = 10 • 9/4= 22,5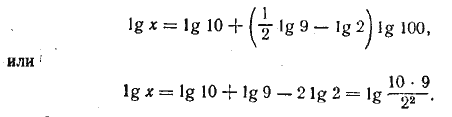
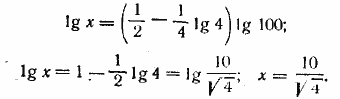
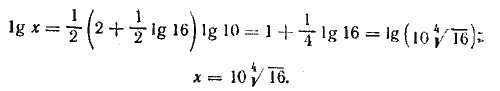
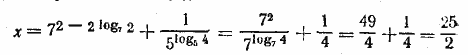
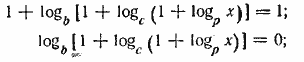
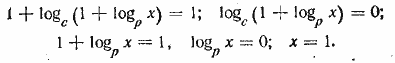
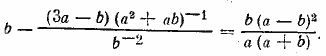
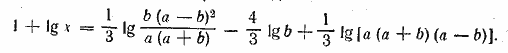
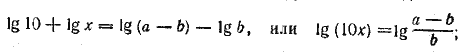
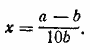 .
.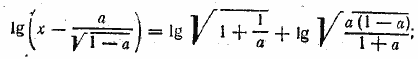
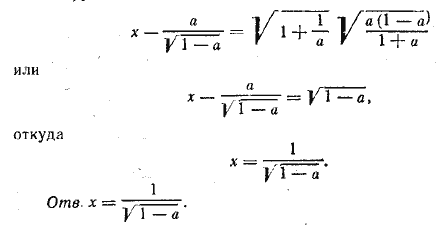
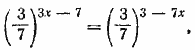
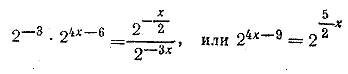
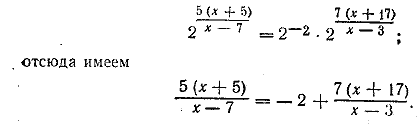
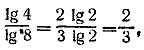 то заданное уравнение можно переписать так:
то заданное уравнение можно переписать так: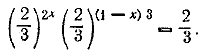
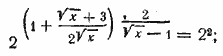
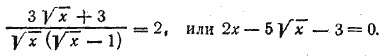
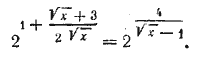
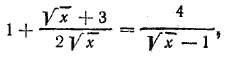
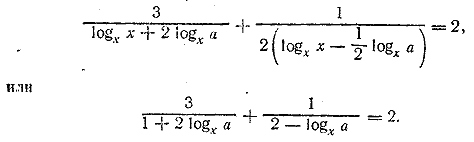
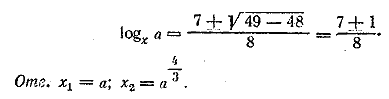
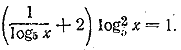
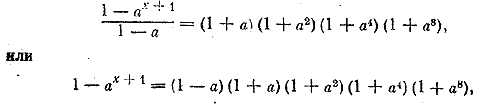
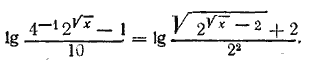
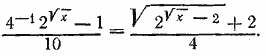
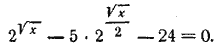
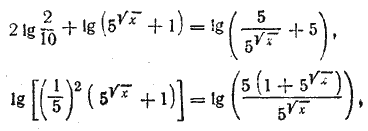
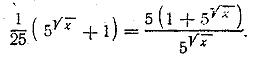 (A)
(A)