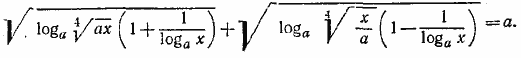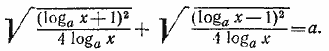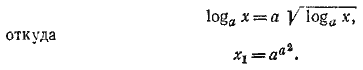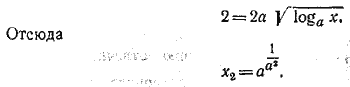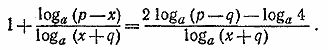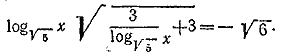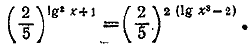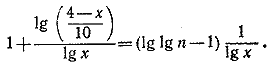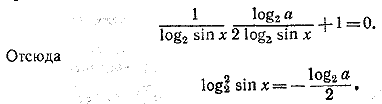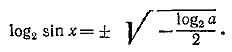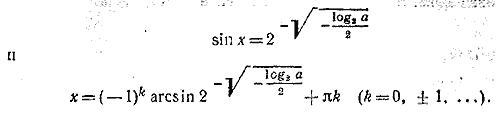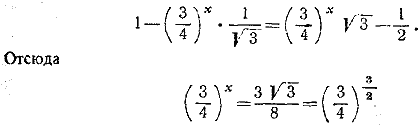|
|
ГЛАВА 4 ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ, ТОЖДЕСТВА. Ответы и решения
Как видно из уравнения, оно имеет смысл только при а > 0, а =/= 1 и b >0, b =/= 1. Для решения уравнения воспользуемся формулой перехода к логарифмам С другим основанием:
(cм. формулу (б) предварительные замечания) Здесь с—произвольное основание (с > 0, с =/= 1). Выбор основания с в данной задаче безразличен, нужно только все логарифмы привести к одному основанию. Можно, например, за общее основание принять а, поскольку а > 0 и а =/= 1 . Тогда уравнение преобразуется к виду
или после упрощения
Отсюда первое решение: logax = 0, т. е. х =1. Второе решение:
__________________________________________________ Перейдем к логарифмам по основанию 2; используя формулу (б) предварительные замечания, получаем:
Это уравнение равносильно следующему:
__________________________________________________ Потенцируя по основанию 2, получаем 9х—1 + 7 = 4 ( 3х—1+ l ). Отсюда (3х—1)2 — 4(3х—1) + 3 = 0. Следовательно, (3х—1)1 = 3, x1 = 2; (3х—1)2 =1, x2=1. __________________________________________________ Перейдем в уравнении к логарифмам по основанию 3. На основании формулы (б) предварительные замечания, будем иметь:
Отсюда ( 1 — log3 x)[ l — ( l + log3 x)2] = 0 и, следовательно, (log3 x)1= l , x1 = 3; (log3 x)2 = 0, x 2=1; (log3 x)3 = —2, x 3= 1/9
__________________________________________________ Перейдем в уравнении к логарифмам по основанию 2. На основании формулы (б) предварительные замечания, будем иметь:
Умножив обе части уравнения на знаменатель, перенесем все члены в левую часть и разложим ее на множители. В результате получим:
Второй из множителей при х > 1, очевидно, положителен и в нуль не обращается. Приравнивая первый множитель нулю, мы устанавливаем, что исходное уравнение при х > 1 имеет, и притом единственный, корень х = 2.
__________________________________________________ Перейдем в уравнении к логарифмам по основанию а (а > 0 и а =/= 1, в противном случае выражение В силу формулы (б) предварительные замечания, получаем:
Отсюда находим: 1) loga2x = 0, x = 1/2 — не удовлетворяет исходному уравнению (логарифм по основанию 1 числа а не существует); 2) loga ax = loga(a2 √x ), х = a2 . Ответ: х = a2. __________________________________________________ Используя равенство logb[ x (2 1g a — x)] =2. Отсюда после потенцирования получаем: х2—21g a • x + b2=0. Решив это уравнение, найдем: x1,2 = 1g a ± √1g2 a — b2 При а > 10b оба корня оказываются вещественными и положительными и, как нетрудно проверить, удовлетворяют исходному уравнению. При а < 10b уравнение не имеет корней. __________________________________________________ Перейдя в уравнении к логарифмам по основанию а, мы приведем его к виду
После дальнейших преобразований получаем:
Учитывая, что квадратные корни понимаются здесь в арифметическом смысле, можно данное уравнение записать так: | loga x + l | + | loga x — l | = 2a √loga x (1) Рассмотрим теперь два случая: 1) Предположим, что loga x > l. (2) Тогда уравнение (1) принимает вид
Легко видеть, что условие (2) удовлетворяется при этом лишь в случае а > 1. 2) Предположим, что 0< loga x < 1. (3) Тогда уравнение (1) принимает вид
Заметим, что условие (3) выполняется лишь тогда, когда a > l. Так как заведомо a =/= 1 (иначе бы исходное уравнение потеряло смысл), то и второй корень х2 существует лишь при условии a > 1. Мы исчерпали все возможности, так как значения х, при которых loga x < 0, очевидно, не могут удовлетворить
уравнению (1). Таким образом, при a > 1 рассматриваемое уравнение имеет два корня: При 0 < a < 1 уравнение корней не имеет. __________________________________________________ Имеем lg (√x+1 + 1) = lg (x —40). Полагая √x+1 = t , получаем после потенцирования уравнение t2 — t —42 = 0. Его корни: t1 =7 и t2 = —6. Так как t = √x+1 > 0, то t2 отбрасываем. Корню t1 соответствует значение x = 48. Проверкой убеждаемся, что оно удовлетворяет исходному уравнению. Таким образом, уравнение имеет единственный корень x = 48. __________________________________________________ Переходя в уравнении к логарифмам по основанию а, получаем: Отсюда после упрощений и потенцирования приходим к квадратному уравнению (x + q)(p — x)= 1/4(p — q)2 Корни этого уравнения имеют вид x1 = 1/2 (p — q) + √pq , x2= 1/2 (p — q) — √pq . Легко проверить, что оба корня удовлетворяют неравенству p > x1,2 > —q, а следовательно, и исходному уравнению. После несложных преобразований, использующих формулу перехода от одной системы логарифмов к другой, приводим данное уравнение к виду
Положив t2 + t — 2 = 0. Его корни: t1 = —2 и t2 = 1. Первому корню отвечает значение x =1/5 которое, как легко проверить, удовлетворяет и исходному уравнению. Второму корню отвечает значение x =√5, которое исходному уравнению не удовлетворяет. __________________________________________________ Пользуясь тем, что 0,4 = 2/5 , а 6,25 = ( 5/2 ) 2, приведем исходное уравнение к виду
Приравнивая показатели, получаем уравнение lg2 x — 6 lg x + 5 = 0, решив которое, найдем! (lg x)1 = l , x1 =10 ; (lg x)2 = 5, x2 = 105. __________________________________________________ Перейдя в уравнении и логарифмам по основанию 10, получим:
Отсюда после простых преобразований придем к уравнению ,
После потенцирования будем иметь: x2 — 4x + 1g n = 0, откуда x1,2 = 2 ± √4 —1g n. Несложное исследование приводит теперь к следующим результатам. а) Если 0 < n < 104 и n =/= 103, то уравнение имеет два различных корня: x1 = 2 + √4 —1g n и x2 = 2 — √4 —1g n. б) Если n = 103, то имеется лишь один корень x = 3 (x = 1 приходится отбросить); при n = 104 получаем также один корень x = 2. в) Если, наконец, n > 104, то корней нет. __________________________________________________ Перейдем в уравнении к логарифмам по основанию 2. В результате получим уравнение
Так как величина, стоящая слева, строго положительна (sin x=/=1, иначе бы символ logsin x2 потерял смысл), то log2 a < 0 и, следовательно, при а > 1 уравнение вообще не имеет решений. Считая 0 < а< 1, получаем:
Знак плюс перед радикалом отбрасываем, так как log2 sin x < 0. Тогда
Легко видеть, что вся эта бесконечная серия значений х удовлетворяет исходному уравнению. __________________________________________________ Разделив обе части уравнения на 4х, найдем:
и, следовательно, x = 3/2 __________________________________________________ |
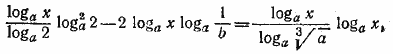
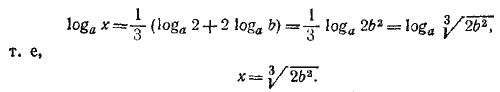
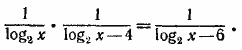
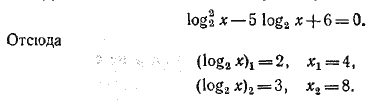
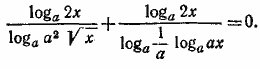
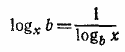 , преобразуем исходное уравнение в эквивалентное:
, преобразуем исходное уравнение в эквивалентное: