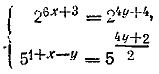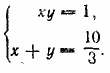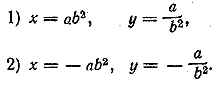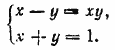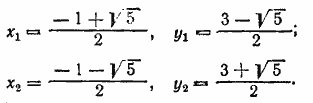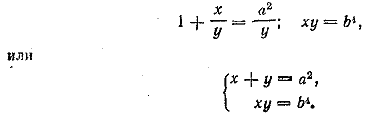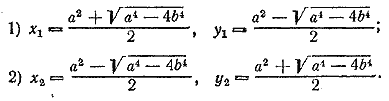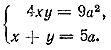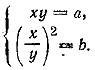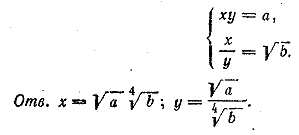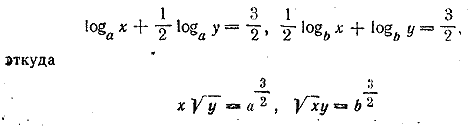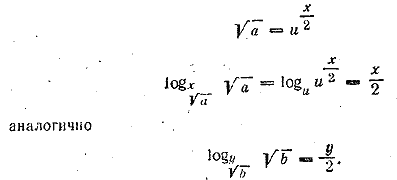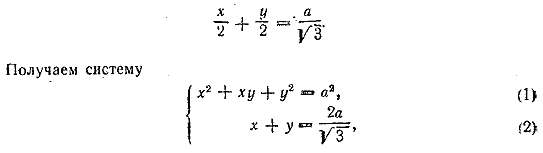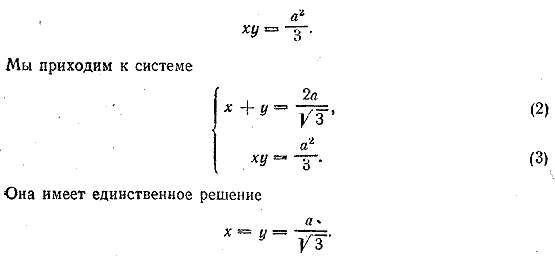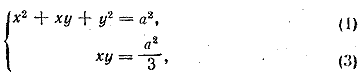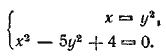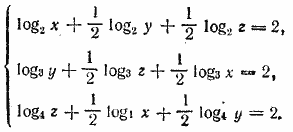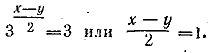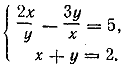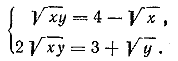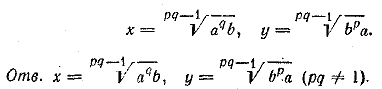|
|
ГЛАВА 4 ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ, ТОЖДЕСТВА. Ответы и решения
Заданные уравнения можно представить в виде
Приравнивая показатели степени, получаем систему
Отв. x = 3/14; y =1/14 __________________________________________________ Потенцируя первое уравнение, получим систему уравнений
Отв. x1 = 3, у1 = 1/3 ; x2 = 1/3, у2 = 3. __________________________________________________ В алгебре обычно рассматриваются только логарифмы положительных чисел при положительных основаниях; иначе число может не иметь (действительного) логарифма. Поэтому будем считать, что известные величины а и b (основания логарифмов) положительны; неизвестные величины х у («числа») также должны быть положительными. Потенцируя, находим ху = a2, x/y = b4 Эта система имеет два решения:
Но второе решение не годится, так как при положительных значениях а , b оно дает отрицательные значения х и у. Отв. __________________________________________________ Потенцируя, получим систему
из второго уравнения у = 7/9 x; подставляя в первое уравнение, будем иметь два решения: 1) x1 =9, y1 = 7; 2) x2= — 9, y2 = —7. Второе решение не годится, так как тогда х + y < 0 и х — y < 0 (см. решение задачи 558). Отв. х = 9; у =7. __________________________________________________ Потенцируя, будем иметь
Эта система имеет два решения:
При первом решении имеем х — y = ху = —2+ √5 > 0. При втором получаем х — y = ху = —2—√5 < 0. Второе решение не годится, так как основание логарифмов ху должно быть положительным (см. задачу 558). Отв. __________________________________________________ Потенцируя, получим систему
Эта система имеет два решения:
Считая данные величины а и b положительными (как основания логарифмов), мы должны различать два случая: 1) a4 < 4b4, т. е. а < √2b и 2) a4 > 4b4, т. е. а > √2b . В первом случае система не имеет решения, так как х и у — мнимые, числа. Во втором случае х и у не только действительны, но и положительны, так как и сумма х + у = a2, и произведение ху = b4 положительны. Отв. __________________________________________________ Потенцируя первое уравнение, получим систему
Оба ее решения годны. Отв. 1) x1 = a/2, y1 = 9/2 a 2) x2 = 9/2 а , y2= a/2 __________________________________________________ Так как во втором уравнении неизвестные х и у входят под знаком логарифма, то оба они положительны (если решение существует). Что касается величины а, то она может быть и отрицательной (ибо под знаком логарифма стоит положительное число a2). Однако в этом случае вместо равенства lg (a2) =2lg а надо написать lg (a2) =2lg |а| . Для краткости обозначим lg |а| = А; Логарифмируя первое уравнение заданной системы, получим систему X+Y=2A, X2+Y2=10A2 Возвышая первое уравнение в квадрат и вычитая второе, получим XY= —3A2 , так что имеем равносильную систему X+Y=2A, XY= —3A2 Следовательно, X и Y —корни уравнения z2—2Az—3A2 = 0. Значит, одно решение есть Х=3A, Y=— А, т. е. х = |а|3 , у = 1/|a| Другoe решение: х = 1/|a| , у = |а|3. Проверка показывает, что оба решения годятся. Отв. х1 = |а|3 , у1 = 1/|a| ; х2 = 1/|a| , у2 = |а|3 __________________________________________________ Из второго уравнения имеем у — х = (√2)4 = 4 Следовательно, y = х+4. Подставив в первое уравнение, получим 3x • 2x+4 = 576, или 6x • 24 = 576. Отв. x = 2; y = 6. __________________________________________________ Данную систему можно записать так:
Так как оба числа х и у должны быть положительными то получаем систему
__________________________________________________
Перемножая эти уравнения, будем иметь Отв. __________________________________________________ Решение аналогично предыдущему. Отв. __________________________________________________ Пользуясь формулой (а) предварительные замечания, запишем первое уравнение так: т .е. u = v Подставляя во второе уравнение , будем иметь u 2 + u —12=0. Годится только положительное решение (см. решение задачи 558). Отв. u = v = 3. __________________________________________________ Обозначим x√a = и; тогда
Следовательно, второе уравнение можно записать так!
равносильную данной. Возведем уравнение (2) в квадрат. Получим
Вычитая (1) из (2а), найдем
Замечание. При возведении какого-либо уравнения в квадрат мы можем получить лишние решения. Так и есть в данном случае: уравнение (2а) имеет лишние решения по сравнению с (2). Например, значения Но если бы мы взяли не систему (2) — (3), а систему (1) —(3), т. е. систему
то она не была бы равносильна данной. Действительно, кроме рeшения Поэтому в случаях, когда мы возводим одно или несколько уравнений в квадрат, всегда необходимо либо исследовать вопрос о равносильности, либо с помощью подстановки проверить, какие решения годятся, а какие нет. Отв. __________________________________________________ Принимая во внимание формулу (б) предварительные замечания,, будем иметь log4 х = 1/2 log2 х; вследствие этого первое уравнение приводится к виду х = у2. Решаем систему
Отв. x1= 4, y1=2; x2 = 1, y2=1. __________________________________________________ С помощью формулы (б) предварительные замечания данную систему можно записать в виде
Потенцируя, находим
Перемножая все уравнения (а), получим (xyz)2=4•9•16, откуда xyz = 24 (б) (берем арифметическое значение корня, так как по смыслу данных уравнений х, у, z должны быть положительны). Возводим каждое из уравнений (а) в квадрат и делим на (б), Отв. x = 2/3, y=27/8, z = 32/3. __________________________________________________ Из первого уравнения находим
Значит, х + у = 3 • 22=12. Отв. х = 7; у = 5. __________________________________________________ Заданная система приводится к следующей:
Разделив второе уравнение на первое, получим х — у = 4x/7 Решив систему х + y =70/x и х — у = 4x/7 , будем иметь x1= 7, y1=3; x2=—7, y2=—3. Корни x2, y2 не удовлетворяют второму уравнению заданной системы, так как числа x2+y2 и x2—y2 отрицательны. Отв. х = 7; у = 3. __________________________________________________ Представим данную систему в виде
Отсюда получаем
Введем обозначение x/y = t ; тогда из первого уравнения будем иметь 2t2—5t—3 = 0; t1 = 3, t2 = — 1/2, т. е. x/y = 3 или x/y = — 1/2 Отсюда находим выражения х = 3у и х= —1/2y , подставляя их во второе уравнение, найдем x1 = —2, y1 = 4 ; x2 = 3/2 , y2 =1/2 Отв. x1 = —2, y1 = 4 ; x2 = 3/2 , y2 =1/2 __________________________________________________ Данная система приводится к следующей:
Из первого уравнения (см. решение задачи 574) находим x/y = 3 или x/y = —1/2. Второе уравнение дает x1 = 3/2 , y1 =1/2 ; x2 = —2, y2 = 4 . Значения x2, y2 не подходят. Отв. x = 3/2 , y =1/2 __________________________________________________ Данная система приводится к следующей:
Введя обозначения √x = и; √y = v, получим иv = 4—u; 2иv = 3+v. Отв. x1 = 4 , y1 =1 ; x2 = 1, y2 = 9 __________________________________________________ Перепишем данную систему в виде ay = x p, bx = y q. Так как х и у должны быть положительными (как основания логарифмов), то исходная система может иметь решения лишь при положительных значениях а и b. Из первого уравнения найдем Если pq =1, то эго уравнение либо вовсе не имеет решений (при aqb =/= l), либо является тождеством (при aqb = l). В последнем случае исходная система имеет бесчисленное количество решении (х — произвольное число, а __________________________________________________
|
,или xy = аb. Последнее уравнение делим на каждое из предыдущих.
(2а)
удовлетворяют уравнению (2а), но не удовлетворяют уравнению (2). Иными словами, уравнение 
не равносильно уравнению
; оно равносильно двум уравнениям: 
Тем не менее данная система и система уравнении 
равносильны, потому что в последнюю систему входит уравнение 
она имела бы еще решение 
.
а из второго х+у = 3 • 2х—y, следовательно, 
; подставляя во второе уравнение, получаем x pq=aqbx . Oт брасывая корень х = 0 (х должно быть положительным), получаем уравнение x pq—1= aqb. 
. Если pq =/=1, то получаем решение: