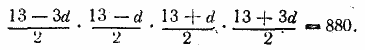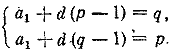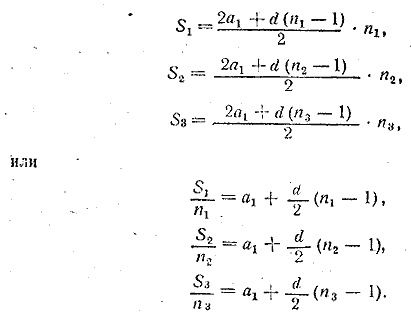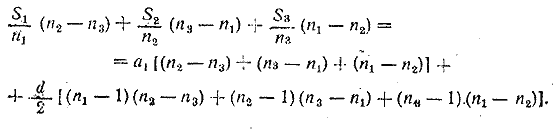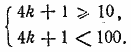ГЛАВА 6

ПРОГРЕССИИ

Арифметическая прогрессия

Ответы и решения

638.По условию a₁= 5, d =4.   Подставляя эти   значения в  (3), получим после некоторых преобразований уравнение

2п² + 3п — 10 877 = 0.

Корни его: n₁ = 73 и  n₂ = — 74,5;  из   них   годится   только   первый.

Отв. 73 члена.

__________________________________________________

639.По условию

a₁+ (a₁+d ) + (a₁+2d) + (a₁+3d) = 26,

a₁(a₁+d) (a₁+2d) (a₁+3d) =880.

Первое уравнение дает 4a₁+ 6d = 26, откуда  Подставляя во второе уравнение и упрощая выражения в скобках, получаем

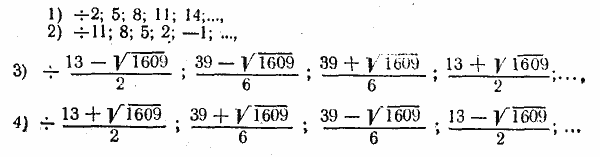
Освобождаясь от знаменателя и перемножая числители (удобнее всего умножить первый числитель на четвертый и второй на третий), находим:

9d ⁴ — 1690d ² + 14481 = 0.

Обозначим через d' d", d"', d"" корни этого биквадратного уравнения, находим

из уравнения  находим соответствующие значения первого члена:

Отв. Задача имеет четыре решения:

__________________________________________________

640.

Выражаем   а_р  и  a_q  через   a₁ и  d    по   условию   получим систему уравнений

Отсюда находим d = —1  и a₁ = p + q—1. По формуле  (1)  находим:

а_n = (p + q — l) — ( n —l ) = p + q — n.

Отв.    а_n = p + q — n.

__________________________________________________

641.

Натуральные двузначные числа составляют арифметическую прогрессию с разностью    d = l ; при этом первый член a₁ =10, а последний а_n = 99.  По формуле   (1)   находим  число членов  n = 90.

Формула (2) дает:

Отв. 4905.

__________________________________________________

642.

Обозначим нечетные числа через п,  (п +2),  (п + 4), (п + 6). Тогда заключенные между ними четные числа будут (п+ 1),  (п+3), (п + 5). Согласно условию

п²+(п+2)²+(п+4)²+(п+6)² = (п +1)²+(п +3)²+(п + 5)²+48,

или

п²+[(п +2)²— (п + l)²] + [(п + 4)²— (п +3)²] +  [(п + 6)²— (п + 5)²] — 48 = 0,

откуда

п² + (2п+3) + (2п+7) + (2п +11) — 48 = 0,

или

п² + 6п —27=0.

Отсюда    п =3 или п = —9.

Отв. 1) 3;   5;   7;   9    или    2) —9; —7; —5; —3.

__________________________________________________

643.

Члены a₂; a₄;  a₆ ...;  a₂₀ составляют арифметическую прогрессию с разностью 2d и числом членов 10. Применяя формулу (3) (где нужно взять a₂  вместо a₁ и 2d вместо d ), найдем

т. е.

a₂ + 9d =25.

Подставляя сюда a₂ = a₁ + d , имеем

a₁ + 10d = 25.                                        (а)

Таким  же   образом,  исходя   из   прогрессии  -:-  a₁; a₃;  a₅ ...;  a₁₉

найдем

a₁ + 9d  = 22.                                            (б)

Из (а) и (б) можно найти a₁ и d, а затем все члены прогрессии. Но так как требуется найти только средние члены, т. е. a₁₀= a₁+9d   и  a₁₁= a₁+10d , то (а) и (б) сразу дают a₁₀ = 22 и a₁₁ = 25.

Отв. Средние члены равны 22 и 25.

__________________________________________________

644.

Введем обозначения b₁=(а+х)², b₂=(а²+х²), b₃=(а—х)². Находим b₂—b₁= b₃—b₂=—2ах.   Следовательно,    члены  b₁, b₂,  b₃ образуют   арифметическую   прогрессию с    разностью d =—2ах. По формуле (3) имеем

Отв.    S_n = [a² + (3 — п) ах + х²] п.

__________________________________________________

645.

По формуле (3) имеем

Умножаем    полученные    равенства    соответственно    на     (n₂— n₃), (n₃— n₁)  и   (n₁— n₂)  и складываем произведения, после чего найдем

Выражения в квадратных скобках тождественно равны нулю, следовательно,

что и требовалось доказать.

__________________________________________________

646.

Из условия следует, что   S₁₀= 5S₅.   Выразив    S₅ и  S₁₀  по формуле (3) и учитывая, что по условию а₁  = 1, найдём

откуда d = —3.

Отв. -:-  +1; —2; —5; —8; ...

__________________________________________________

647.

По условию

Так как п =/= 0, то, сократив это: уравнений на п , получим 2а₁+ dп — d = 6п  или

2а₁— d = (6—d)п.                                     (а)

По условию равенство (а) должно удовлетворяться при любом значении п, но левая часть (а) не содержит п, тогда как правая часть будет менять значение с изменением п, если только множитель 6 — d не равен нулю. Лишь в случае 6 — d = 0 правая часть не зависит от п (равна нулю),   поэтому   мы должны    иметь d = 6.

Тогда из (а) находим 2а₁— d  = 0, т. е.   а₁ = ^d/₂ = 3.

Отв. -:- 3; 9; 15; 21; ...

__________________________________________________

648.

Числа, которые при делении на 4 дают в остатке 1, имеют вид 4k+1  (k —любое натуральное число). Они образуют арифметическую прогрессию с   разностью    4. Первое из   двузначных   чисел этого вида есть 13   (оно получается  при k = 3);    последнее есть 97. По  формуле   (1),  где  а₁ =13,  а_n=97,   d = 4,   находим   n = 22.   По формуле (3) найдем искомую сумму.

Для определения, при каких значениях k числа вида 4k +1 будут двузначными, можно было бы воспользоваться системой неравенств

Из этой    системы    находим 2¹/₄ < k <  24³/₄:следовательно,   k может иметь значения, равные 3, 4, 5, ... , 24, число которых n =(24—3)+1=22.

Oms. 1210.

__________________________________________________