|
ГЛАВА 6
ПРОГРЕССИИ
Геометрическая прогрессия
Ответы и решения
649. Среднее геометрическое двух (положительных) чисел а и b есть положительное число х, определяемое из пропорции а : х = х : b. Вставить три средних геометрических между числами 1 и 256 — значит найти три числа u2 , u3 , u4, удовлетворяющих условиям:
1 : u2 = u2 : u3 = u3 : u4 = u4 : 256.
Значит, числа u1= 1, u2, u3, u4 и u5 = 256 образуют геометрическую прогрессию. По формуле n -го члена прогрессии 256 = 1•q4. Это уравнение имеет один положительный корень q4 = √256 = 4 (— 4; + 4i ; —4i не годятся). Теперь по той же формуле находим: u2 = 4; u3 =16; u4 = 64.
Отв. 4; 16; 64.
__________________________________________________
650. По условию u1+ u2 =52 и u22 = 100, или u2 = ±10. По свойству геометрической прогрессии u1u3 = u22= 100; следовательно, u1 и u3 — корни уравнения u2—52u +100 = 0. Отсюда найдем: u1= 50 и u3 = 2 или u1 = 2 и u3 = 50.
Отв. Числа будут: 1) 50; 10; 2 или 2) 50; —10; 2, или те же числа в обратном порядке.
__________________________________________________
651. По условию: 1) u3 — u1= 9 и 2) u5— u3=36.
Применяя формулу un = u1qn — 1, запишем эти уравнения в виде:
1) u1q2 —u1= 9; 2) u1q4 — u1q2 =36.
Деля уравнение 2) на 1), получим q2 = 4; отсюда q = ±2; из 1) находим: u1= 3.
Отв. 1) -::- 3; 6; 12; 24; 48; ... 2) -::- 3; —6; 12; —24; 48; ...
__________________________________________________
652. По условию u1 + u4= 27 и u2u3 = 72; но так как 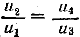 или u2u3 = u1u4, то имеем систему двух уравнений: или u2u3 = u1u4, то имеем систему двух уравнений:
1) u1 + u4= 27 и 2) u1u4 = 72,
откуда u1 = 3 и u4 = 24 или u1 =24 и u4=3. Из формулы u4 =u1q3 находим соответственно q = 2 или q = 1/2.
Отв. 3; 6; 12; 24 или в обратном порядке: 24; 12; 6; 3.
__________________________________________________
653. По условию 1) u1 + u4 =35 и 2) u2 + u3 = 30. Так же, как в задаче 651, для определения q получаем уравнение
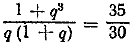
или по сокращении
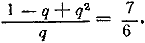
Находим:
1) q = 3/2; u1 = 8; 2) q = 2/3; u1 = 27.
Получаем две прогрессии:
1) -::- 8; 12; 18; 27; 40,5; ....
2) -::- 27; 18; 12; 8; 5 1/3; ... ,
у которых первые четыре члена одинаковы, но идут в обратном порядке.
Отв. 8; 12; 18; 27.
__________________________________________________
654. Во второй дайной сумме заменяем каждый член через предыдущий, умноженный на q (согласно определению геометрической прогрессии); получим
u1q + u2q + u3q + u4q + u5q = 62
или
q(u1 + u2 + u3 + u4 + u5) = 62.
По условию выражение в скобках равно 31; следовательно, q = 2. Пользуясь формулой 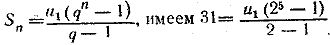 откуда u1= 1. откуда u1= 1.
Отв. -::- 1; 2; 4; 8; ...
__________________________________________________
655.По условию имеем:
1) u2 + u3 + u4 + u5 =19,5, 2) u1 + u2 + u3 + u4 = 13.
Задача аналогична предыдущей.
Отв. u1= l,6 и u5 = 8,l.
__________________________________________________
656. Члены u4 и u6 — равноотстоящие от начала и конца;
поэтому u4u6 =u1u9. Так как по условию u1u9 = 2304, тo u4u6 =2304; кроме того, по условию u4 + u6 =120. Из этих двух уравнений находим
u'4 =24; u'6=96; u''4=96 и u''6= 24.
Возьмем первое решение. По формуле un = u1qn — 1 имеем:
1) 24 = u1q3 ; 2) 96 = u1q5 .
Разделив 2) на 1), находим q2 = 4, откуда q = 2 или q = — 2. В первом случае уравнение 1) дает u1 =3, во втором случае u1 = —3.
Девять членов прогрессии будут в первом случае:
3; 6; 12; 24; 48; 96; 192; 384; 768;
во втором:
—3; 6; —12; 24; —48; 96; —192, 384; —768.
Взяв решение u''4= 96 ; u''6= 24., найдем те же два ряда членов, но в обратном порядке.
Отв. 1) u1 =3; q = 2;
2) u1= —3; q =—2;
3) u1 = 768; q = 1/2;
4) u1 = —768; q = — 1/2.
__________________________________________________
657.По условию 1) u1 + u2 + u3 =126 и 2) u1u2u3= 13 824.
Так как u2 есть средняя пропорциональная между u1 и u3 , то u1u3 = u22; поэтому вместо 2) можно написать u23= 13 824, откуда u2 = 3√13 824 . В данном случае, разлагая 13 824 на множители, легко найти, что u2 = 24. Подставляя в 1) и 2), получаем систему уравнений:
u1 + u3 =102; u1u3 = 576.
Решения ее: u1= 6; u3 = 96 и u1= 96; u3 = 6.
Получаем две прогрессии: -::- 6; 24; 96 и -::- 96; 24; 6, отличающиеся, только порядком членов.
Отв. 6; 24; 96.
__________________________________________________
658. Из условия следует, что сумма членов, стоящих на четных местах, в два раза больше суммы членов, стоящих на нечетных местах, т. е.
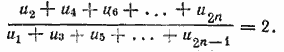
Заменяя члены u2; u4; u6; ...; u2n выражениями u2 =u1q; u4 = u3q; ... .., u2n = u2n—1q, находим q=2.
Отв. Знаменатель прогрессии равен 2.
__________________________________________________
|