|
ГЛАВА 6
ПРОГРЕССИИ
Бесконечно убывающая геометрическая прогрессия.
Ответы и решения
659.Для доказательства того, что данные числа образуют геометрическую убывающую прогрессию, надо проверить, будут ли равны отношения 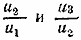 и будут ли они меньше 1. Имеем: и будут ли они меньше 1. Имеем:
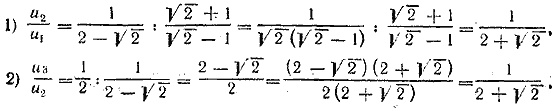
Так как 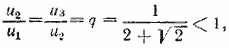 то данные числа образуют геометрическую убывающую прогрессию. По формуле ее суммы находим то данные числа образуют геометрическую убывающую прогрессию. По формуле ее суммы находим
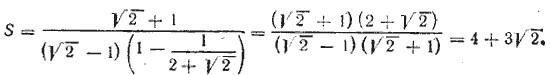
Отв. S = 4 + 3√2 .
__________________________________________________
660. Как в предыдущей задаче, находим, что выражение в квадратных скобках равно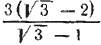 Все выражение тогда примет вид Все выражение тогда примет вид
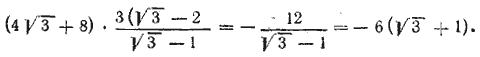
Отв. — 6(√3 + 1)
__________________________________________________
661. По условию
u1 = 4 и u3— u5 = 32/81
По формуле un = u1qn — 1 из второго равенства получаем
u1q2— u1q4 = 32/81
Учитывая, что u1 = 4, получаем биквадратное уравнение 81q4—81q2 + 8 = 0; его корни: 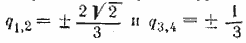 Отрицательные корни не годятся, так как по условию все члены положительны, положительные корни годятся оба, так как они меньше единицы. Получим две бесконечно убывающие прогрессии. Отрицательные корни не годятся, так как по условию все члены положительны, положительные корни годятся оба, так как они меньше единицы. Получим две бесконечно убывающие прогрессии.
Отв. S' = 12 (3 + 2√2 ) и S" = 6.
__________________________________________________
662. По условию
u1 + u4=54 и u2+u3=36.
С помощью формулы un = u1qn — 1 получим систему двух уравнений:
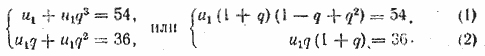
Разделив (1) на (2), получим уравнение
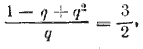
из которого найдем q1 = 2 и q2 = 1/2. Годится q2 = 1/2 < 1. Находим
из (2) u1= 48.
Отв. S=96.
__________________________________________________
663. Первый способ. По условию
1) u1 + u3 + u5 + ...= 36,
2) u2 + u4 + u6+...= 12.
Члены первой и второй сумм составляют также бесконечно убывающие прогрессии, знаменатель которых одинаков и равен q2, первый член в первой прогрессии равен u1, а во второй u2, т. е. u1q. Выражая суммы первой и второй прогрессий по формуле суммы бесконечно убывающей прогрессии (где вместо q берем q2, а вместо u1 во втором случае берем u1q), получим:
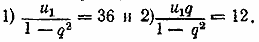
Деля 2) на 1)-, получим: q = 1/3, а из первого уравнения находим u1 =32.
Второй способ. Так как u2 = u1q, u4 = u3q и т. д., то вместо u2 + u4 + u6+...= 12 получим u1q +u3q+u5q+... = 12, или
q(u1+u3+u5+...) = 12. (1)
Разделив на (1) условие u1 + u3 + u5 + ...= 36, найдем q = 1/3
С другой стороны, сумма всех членов прогрессии есть 12+36=48 По формуле суммы бесконечно убывающей прогрессии имеем 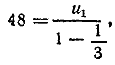 , откуда u1 =32. , откуда u1 =32.
Отв. -::- 32; 32/3; 32/9; ...
__________________________________________________
664. По условию
u1 + u2 + u3 + ... = 56; u12 + u22 + u32 + ... = 448.
Слагаемые второй суммы образуют также геометрическую бесконечно убывающую прогрессию с первым членом u12 и знаменателем q2. Выражая суммы этих прогрессий, получим
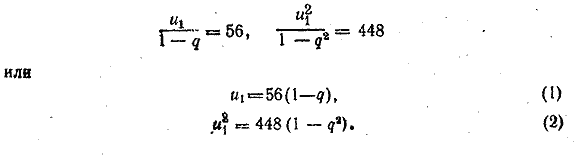
Деля (2) на (1), находим
u1= 8( l + q ). . (3)
Исключая u1 из уравнений (1) и (3), получаем
8 (1+q) = 56(1—q),
откуда q = 3/4 Из (1) находим u1= 14.
Отв. u1= 14, q = 3/4
__________________________________________________
665. Задача решается аналогично предыдущей. Для определении u1 и q получим систему уравнений:

После исключения из этих уравнений u1 получим уравнение
3q2—10q +3=0. Из двух корней его годится только q = 1/3 (другой q = 3 больше единицы). Из уравнения (1) находим u1= 2.
Отв. -::- 2; 2/3 ; 2/9 ; ...
__________________________________________________
666. Задача решается аналогично задачам 664, 665. Для определения u1 и q получим систему уравнений:
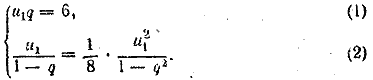
Уравнение (2) равносильно уравнению u1= 8( l + q )
Исключая u1 из системы u1q = 6, u1= 8( l + q ), получаем уравнение 4q2+4q—3 = 0.
Из двух его корней q1= — 3/2, q2= 1/2 годится только второй, так как абсолютная величина первого больше единицы. Из (1) находим u1= 12.
Отв. -::- 12; 6; 3; ...
__________________________________________________
|