ГЛАВА 7

СОЕДИНЕНИЯ   И  БИНОМ   НЬЮТОНА

Ответы и решения

708.Записав отдельно  отношения первого   члена пропорции ко второму и второго к третьему, после сокращения получим:

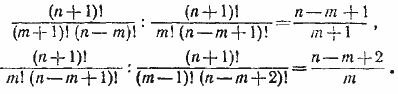
В силу условия задачи мы приходим к двум уравнениям:

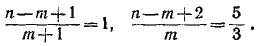
Решив их совместно, найдем т = 3 , n = 6.

__________________________________________________

709.Имеем:

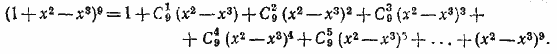
Рассматривая слагаемые правой части, легко заметить, что x⁸содержится лишь в четвертом и пятом членах. Используя это, без труда находим коэффициент при x⁸.

Он равен   3C ³₉+ C ⁴₉.

__________________________________________________

710.Слагаемые  данной  суммы  образуют  прогрессию со знаменателем 1 + х. Поэтому

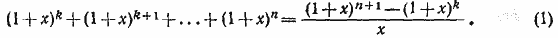
Записав эту же сумму в виде многочлена

a₀  +  a₁x  +   • • • + a_mx^m + .. .+ a_nxⁿ,

и раскрыв скобки в правой части равенства (1), получим: если т < k, то

a_m =C ^m+1_n+1  — C ^m+1_k

если же m  >  k, то

a_m =C ^m+1_n+1

__________________________________________________

711.Из условия задачи следует:

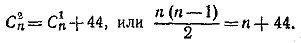
Решив это уравнение относительно п, найдем п = 11. Общий член разложения

можно записать в виде

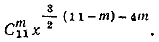
По условию задачи  ³/₂(11— m) — 4m = 0, откуда m = 3. Следовательно, искомый член равен C ³₁₁

__________________________________________________

712.   Положим  x + ⁶/_x = и, тогда

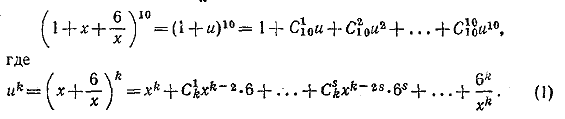
Для слагаемого, не содержащего х в выражении (1), должно удовлетворяться условие     k—2s = 0; следовательно, это слагаемое будет равно C ^s_2s• 6^s. Собирая все такие члены, найдем, что слагаемое, не содержащее х в первоначальном выражении, будет равно

__________________________________________________

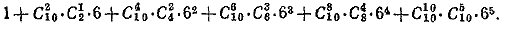
713. Неравенства  T_k+1 > T_k и  T_k+1 > T_k+2  после  упрощений принимают вид

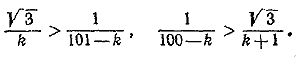
Решив каждое из них относительно k, получим:

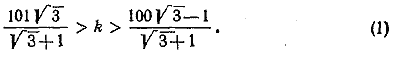
Левая и правая части  неравенства   (1) — числа не целые, а разность между ними  равна  единице.   Поэтому  существует лишь одно целое число k, удовлетворяющее неравенству (1). Заметив, что 1,72 < √3 < 1,73, прямым вычислением установим что

64,64 > k  > 63,135.

Следовательно, k = 64.

__________________________________________________

714.Общий  член   разложения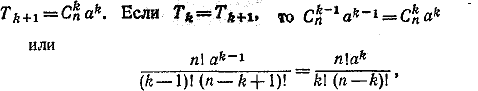   

откуда 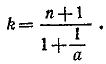   Получаем   искомое   условие:   1+ ¹/_a      должно быть делителем числа n + 1.

Если теперь T_k =  T_k+1 = T_k+2,  то это эквивалентно равенствам

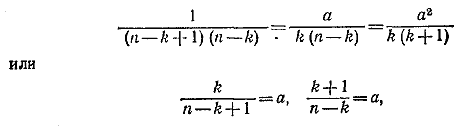
что приводит к условию n  +1=0, которое невыполнимо.

__________________________________________________

715.   В разложение  войдут:    членов вида   x_i ³  (  = 1, 2, ..., п),      п(п— 1)   членов   вида   x_i²x_j   (  i, j = 1,  2,  ... , п,   i =/= j )   и, наконец, C ³_n членов вида x_i x_j x_k,   где i ,  j , k — различные  числа.   Таким образом, число различных не подобных членов равно

__________________________________________________

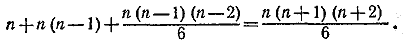
716. Делителями числа q являются, очевидно, числа p₁,    p₂,  ...,  p_k и всевозможные  их  произведения   по два,   по три и т. д. Число таких делителей равно

C ⁰_k+C ¹_k+...+C ^k_k = 2^k.

Так факт, что все полученные делители не равны между собой и что других делителей нет, следует из единственности представления числа в виде произведения простых чисел.

__________________________________________________

717.Подлежащее доказательству равенство имеет вид

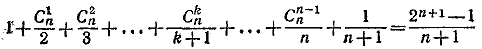
и равносильно равенству

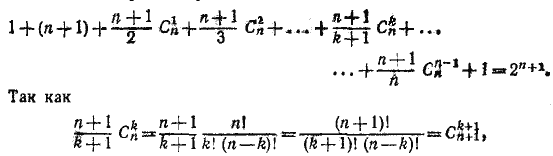
то левая часть последнего равенства равна

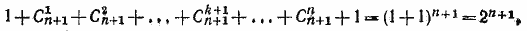
что и требовалось доказать.

__________________________________________________

718.  Общий   член  левой  части   равенства   может  быть  преобразован следующим образом:

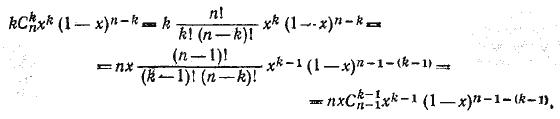
Поэтому   левая   часть   равенства   может  быть   представлена   в   следующем виде:

__________________________________________________

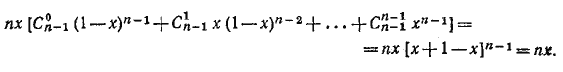
719. Всякое деление  колоды, указанное в условии равносильно извлечению 16 нетузов   из числа 32 нетузов  и двух  тузов  из числа четырех тузов. Первое извлечение можно осуществить C ¹⁶₃₂ способами, а   второе   C ²₄  способами.   Так  как   каждое   извлечение   16  нетузов можно  скомбинировать с любым извлечением  двух  тузов,  то общее число способов указанного деления колоды равно C ¹⁶₃₂ C ²₄.

__________________________________________________

720. Искомое  число  номеров  равно  числу размещений, которые можно  образовать   из   10  цифр по 5, т. е.  равно   10 • 9 • 8 • 7 • 6 = = 30 240.

__________________________________________________

721. Занумеруем   некоторые  п мест  и  будем  образовывать  разбиения, последовательно  заполняя  каждое из указанных мест парой элементов.

На первое место можно выбрать пару C ²_2n способами; после того как первая пара выбрана, вторую можно выбрать C ²_2n—2 способами, третью C ²_2n—4  способами и т. д. В результате мы придем к C ²_2nC ²_2n—2C ²_2n—4  . . . C ²₂ разбиениям, в число которых войдут, однако, и   все   разбиения,    отличающиеся    порядком    расположения   пар.

Следовательно, число интересующих нас разбиений равно

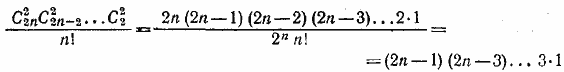
Это произведение сокращенно иногда обозначают символом (2n —1)!!

К тому же результату можно прийти, рассуждая несколько иначе. Обозначим через k_n число разбиений для того случая, когда число элементов равно 2n. Рассмотрим 2n элементов. Поскольку порядок расположения пар несуществен, можно считать первой парой ту, которая содержит первый элемент. Пары, содержащие первый элемент, можно образовать 2n —1 способами. Остальные 2 (n — 1) элементов при выбранной первой паре можно разбить на пары k_n—1 способами. Поэтому k_n = (2n — 1)k_n—1. С помощью этого соотношения легко находим:

k_n= (2n — 1)(2n — 3) . . . 5•3•1.

__________________________________________________

722.   Из  общего  числа п!  перестановок   нам   надлежит  вычесть те, в которых элементы а и b стоят рядом. Чтобы образовать такую перестановку,   нужно  взять   некоторую   перестановку из оставшихся п—2   элементов   (их   всего   (п—2)!)   и   присоединить  к  выбранной перестановке  два   элемента  а и b так, чтобы  они оказались   рядом. Это,   очевидно,   можно   сделать   2 (п—1)   способами   (множитель  2 здесь  связан с тем, что а и b  можно  переставить  местами).   Таким образом,   число  перестановок,   в которых а и b стоят   рядом,   равно 2(п — 2)! (п—1), а интересующее нас число равно

п!—2 (п —1)! = (п—1)! (п—2).

__________________________________________________

723.  Если   среди   вынутых  5 билетов   оказалось   ровно   два   выигрышных,   то  остальные  три—невыигрышные.   Из  8  выигрышных билетов   можно   выбрать   два     C ²₈   способами,   из   50—8 = 42   невыигрышных   билетов   три   можно   выбрать  C ³₄₂   способами.    Каждый способ выбора двух выигрышных билетов может сочетаться с любым из   способов   выбора   трех   невыигрышных.    Поэтому   общее   число способов равно

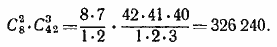
Число способов выбора 5 билетов, при которых, по крайней мере (по меньшей мере), два будут выигрышными, равно сумме числа способов, при которых вынимается ровно два выигрышных, ровно три выигрышных, ровно четыре выигрышных и ровно пять выигрышных билетов. Следовательно, это число равно

__________________________________________________

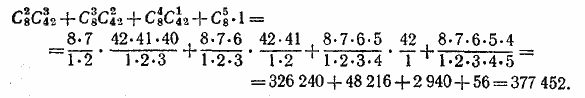
724.  Первое  решение.   Пусть на верхней  прямой  расположено  п точек,   а  на  нижней  m  точек   (рис.   1).   

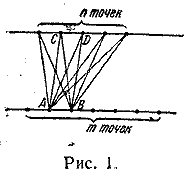
Подразделим  все соединяющие отрезки на пучки отрезков, причем в один пучок объединим все отрезки, соединяющие фиксированную точку нижней прямой (например, А) со всеми точками на верхней прямой. Ясно, что число таких пучков равно т и что число точек пересечения отрезков, принадлежащих каким-нибудь двум пучкам, одно и то же для любой пары пучков. Если это число   обозначим    через   k_n,   то   общее  число  точек пересечения  всех  отрезков будет  равно  произведению k_n на число сочетаний пучков по два, т. е.

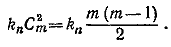
Для   подсчета    числа   k_n   подразделим все отрезки, соединяющие n  точек  верхней   прямой  с двумя  точками   А   и В   нижней   прямой,   на пучки   отрезков, объединив в один пучок два отрезка, соединяющих фиксированную точку верхней прямой (например, С) с точками А и В. Число таких пучков равно п, а число точек пересечения отрезков, принадлежащих двум пучкам, равно единице (точка пересечения диагоналей трапеции ABCD). Поэтому

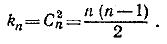
Следовательно, общее число точек пересечения всех отрезков, соединяющих п точек верхней прямой с т точками нижней прямой, равно

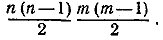
Второе решение. Каждую точку пересечения отрезков можно получить, выбрав две точки на первой прямой, что можно сделать C ²_m способами, и две точки на второй прямой, что можно сделать C ²_n способами. Комбинируя всевозможные пары точек, мы получим

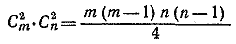точек пересечения.

__________________________________________________

725.  Каждый  параллелограмм  определяется   выбором  двух прямых первой  серии,   что   можно   сделать C ²_n  способами,  и двух прямых второй   серии, что  можно  сделать C ²_m способами.   Таким образом, общее число параллелограммов равно

__________________________________________________

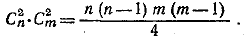
726. Ввиду  того  что  в   данном   алфавите   любому   отдельному знаку (точке или тире) и любой   паре знаков соответствует какая-то буква, число способов, которыми можно прочитать сплошную цепочку из  х  знаков,  не  зависит  от   конкретного   строения   этой   цепочки и равно числу всевозможных разбиений, образующих цепочку знаков на группы из одного или двух рядом стоящих знаков. Обозначим это число через р_п.

Распределим всевозможные способы прочтения данной цепочки из п знаков по двум категориям.

К первой категории отнесем те способы, в которых один первый знак цепочки прочитывается как отдельная буква. Число способов первой категории равно числу способов прочтения цепочки из n—1 знаков (остающихся после отбрасывания первого), т. е. равно   р_п—1.

Ко второй категории отнесем те способы, в которых два первых знака цепочки прочитываются как одна буква. Число способов второй категории равно числу способов прочтения цепочки из п—2 знаков (остающихся  после  отбрасывания  первых двух), т. е. равно   р_п—2  .

Так как всякий способ прочтения данной цепочки принадлежит одной и только одной из двух указанных категорий, то общее число способов равно сумме числа способов первой категории и второй категории, т. е.

р_п =   р_п—1 +   р_п—2                                     (1)

Это равенство представляет собой рекуррентную формулу, по которой можно последовательно вычислить р_п для любого п, если только знать  р₁ и  р₂.

Но в данной задаче р₁ = 1 (для цепочки из oдного знака есть только один способ первой категории) и р₂ = 2 (для цепочки из двух знаков есть два способа: один первой категории и один второй категорий).

Пользуясь формулой (1), последовательно находим:

р₃= р₂+ р₁ = 2 + 1 = 3,

р₄= р₃+ р₂ = 3 + 2 = 5,

р₅= р₄+ р₃ = 5 + 3 = 8,

и т. д.

Окончательно получаем:       р₁₂ = 233.

__________________________________________________